Lause 13.1. ( Lineaarialgebran kokoomalause)
Olkoon 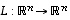 lineaarikuvaus ja
lineaarikuvaus ja 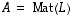 sitä vastaava
sitä vastaava 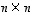 -matriisi. Tällöin seuraavat ehdot ovat keskenään yhtäpitävät (ts. jos yksikin ehto pätee, silloin kaikki muutkin pätevät).
-matriisi. Tällöin seuraavat ehdot ovat keskenään yhtäpitävät (ts. jos yksikin ehto pätee, silloin kaikki muutkin pätevät).
(1) Lineaarikuvaus 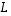 on bijektio.
on bijektio.
(2) Lineaarikuvaus 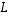 on injektio.
on injektio.
(3) Lineaarikuvauksen 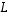 ydin on nollajoukko eli
ydin on nollajoukko eli 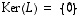 .
.
(4) Lineaarikuvaus 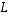 on surjektio eli
on surjektio eli 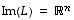 .
.
(5) Lineaarikuvaus 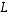 on kannanvaihtokuvaus.
on kannanvaihtokuvaus.
(7) On olemassa 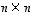 -matriisi
-matriisi 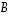 ,
jolle
,
jolle 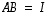 .
.
(8) Yhtälöllä 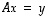 on jokaisella
on jokaisella 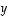 yksikäsitteinen ratkaisu
yksikäsitteinen ratkaisu 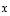 .
.
(9) Homogeenisella yhtälöllä 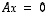 on ratkaisuna vain
on ratkaisuna vain 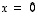 .
.
(10) Yhtälöllä 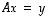 on kaikilla
on kaikilla 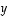 jokin ratkaisu
jokin ratkaisu 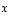 .
.
(11) Matriisin 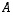 sarakevektorit ovat lineaarisesti riippumattomat.
sarakevektorit ovat lineaarisesti riippumattomat.
(13) Luku 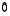 ei ole kuvauksen
ei ole kuvauksen 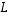 (eikä matriisin
(eikä matriisin 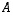 ) ominaisarvo.
) ominaisarvo.
Todistus. Jokainen näistä kohdista on aikaisemmin jossain muodossa todistettu yhtäpitäväksi jonkun muun kohdan kanssa. Seuraavassa ilmoitetaan vain viitteinä ne kohdat, joissa yhtäpitävyys on löydettävissä tai johon sen todentaminen perustuu.
(1) ⇔ (6) : Ks. Käänteismatriisi.
(4) ⇒ (11) : Lause 4.15. Huomaa, että sarakevektorit virittävät täsmälleen arvojoukon.
(11) ⇒ (4) : Lause 4.14. Huomaa, että sarakevektorit virittävät täsmälleen arvojoukon.
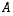 on kääntyvä.
on kääntyvä. 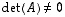 .
.
