Yleinen määrittely
Johdatteluna palautetaan mieliin erään aikaisemman esimerkin tilanne. Kannanvaihdon yhteydessä oli esimerkissä 9.5 tilanne, jossa tason lineaarikuvaukselle 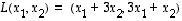 löydettiin sellaiset vektorit
löydettiin sellaiset vektorit 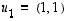 ja
ja 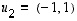 ,
joille
,
joille 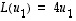 ja
ja 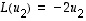 .
Löydettiin siis tason kanta, jonka kantavektorit kuvautuvat vain monikerroikseen. Samanlainen tilanne saatiin aikaan kolmiulotteisessa esimerkissä 9.6. Kun tällainen tilanne tiedetään, koko lineaarikuvauksen hahmottaminen ja hallinta on paljon helpompaa. Voisiko sitten tällaiseen tilanteeseen päästä aina? Ja jos, niin miten? Yritetään seuraavassa vastata tähän. Ensin muutamia nimityksiä.
.
Löydettiin siis tason kanta, jonka kantavektorit kuvautuvat vain monikerroikseen. Samanlainen tilanne saatiin aikaan kolmiulotteisessa esimerkissä 9.6. Kun tällainen tilanne tiedetään, koko lineaarikuvauksen hahmottaminen ja hallinta on paljon helpompaa. Voisiko sitten tällaiseen tilanteeseen päästä aina? Ja jos, niin miten? Yritetään seuraavassa vastata tähän. Ensin muutamia nimityksiä.
Jos lineaarikuvaukselle 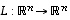 on
on
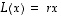
jollekin luvulle 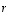 ja jollekin vektorille
ja jollekin vektorille 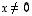 ,
sanotaan, että luku
,
sanotaan, että luku 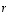 on lineaarikuvauksen
on lineaarikuvauksen 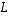 ominaisarvo ja vektori
ominaisarvo ja vektori 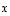 sen
ominaisvektori. Samoja nimityksiä käytetään lineaarikuvausta vastaavalle neliömatriisille
sen
ominaisvektori. Samoja nimityksiä käytetään lineaarikuvausta vastaavalle neliömatriisille 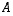 .
Yhtälöä
.
Yhtälöä 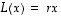 sanotaan
ominaisarvoyhtälöksi.
sanotaan
ominaisarvoyhtälöksi.
Esimerkki 11.2.
Tason lineaarikuvaus 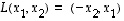 on vuorostaan
on vuorostaan  kierto. Katsotaan löytyykö sille ominaisvektoreita. Nyt
kierto. Katsotaan löytyykö sille ominaisvektoreita. Nyt
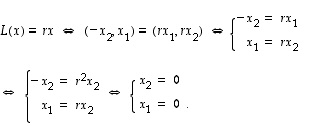
Ei siis ole sellaista vektoria 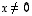 ,
että olisi
,
että olisi 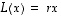 .
Tälle kuvaukselle ei siis ole olemassa ominaisarvoja eikä ominaisvektoreita.
.
Tälle kuvaukselle ei siis ole olemassa ominaisarvoja eikä ominaisvektoreita.

Opiskelutehtävä 42
Muodosta edellisen tehtävän lineaarikuvauksen ominaisvektoreista tason kanta. Mikä matriisi vastaa lineaarikuvausta siinä kannassa? Vastaa siihen sekä suoraan (laskematta mitään!) että tekemällä kyseinen kannanvaihto ja määräämällä sitä kautta kysytty matriisi.
Vinkki tehtävään 42
Ominaisarvoyhtälössä 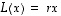 esiintyvät tuntemattomina sekä ominaisarvo
esiintyvät tuntemattomina sekä ominaisarvo 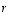 että ominaisvektori
että ominaisvektori 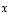 .
Kyseisessä yhtälöryhmässä on siten enemmän ratkaistavia muuttujia kuin yhtälöitä. Tällaisen yhtälöryhmän ratkaiseminen näyttäisi siten kovin epämääräiseltä. Seuraava tulos kuitenkin osoittaa, että mainituista tuntemattomista voidaan ensin ratkaista pelkästään ominaisarvot ilman ominaisvektoreiden laskemista. Ne voidaan laskea sitten jälkeenpäin.
.
Kyseisessä yhtälöryhmässä on siten enemmän ratkaistavia muuttujia kuin yhtälöitä. Tällaisen yhtälöryhmän ratkaiseminen näyttäisi siten kovin epämääräiseltä. Seuraava tulos kuitenkin osoittaa, että mainituista tuntemattomista voidaan ensin ratkaista pelkästään ominaisarvot ilman ominaisvektoreiden laskemista. Ne voidaan laskea sitten jälkeenpäin.
Esimerkki 11.4.
Matriisin
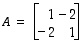
karakteristinen yhtälö on
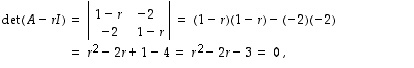
jonka ratkaisuna on
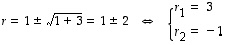 .
.
Määrätään sitten ominaisvektorit. Kun 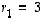 ,
ominaisvektorit saadaan ehdosta
,
ominaisvektorit saadaan ehdosta
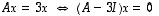 .
.
Ratkaistaan tämä Gaussin ja Jordanin menetelmällä:

Ominaisarvoon 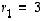 liittyvät ominaisvektorit ovat siis muotoa
liittyvät ominaisvektorit ovat siis muotoa 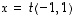 ,
missä
,
missä 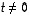 .
.
Ratkaistaan sitten ominaisarvoon 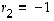 liittyvät ominaisvektorit:
liittyvät ominaisvektorit:

Ominaisvektoreina ovat nyt siis vektorit 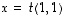 ,
missä
,
missä 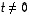 .
.

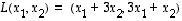 löydettiin sellaiset vektorit
löydettiin sellaiset vektorit 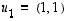 ja
ja 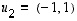 ,
joille
,
joille 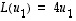 ja
ja 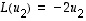 .
Löydettiin siis tason kanta, jonka kantavektorit kuvautuvat vain monikerroikseen. Samanlainen tilanne saatiin aikaan kolmiulotteisessa esimerkissä 9.6. Kun tällainen tilanne tiedetään, koko lineaarikuvauksen hahmottaminen ja hallinta on paljon helpompaa. Voisiko sitten tällaiseen tilanteeseen päästä aina? Ja jos, niin miten? Yritetään seuraavassa vastata tähän. Ensin muutamia nimityksiä.
.
Löydettiin siis tason kanta, jonka kantavektorit kuvautuvat vain monikerroikseen. Samanlainen tilanne saatiin aikaan kolmiulotteisessa esimerkissä 9.6. Kun tällainen tilanne tiedetään, koko lineaarikuvauksen hahmottaminen ja hallinta on paljon helpompaa. Voisiko sitten tällaiseen tilanteeseen päästä aina? Ja jos, niin miten? Yritetään seuraavassa vastata tähän. Ensin muutamia nimityksiä. 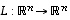 on
on 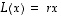
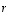 ja jollekin vektorille
ja jollekin vektorille 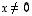 ,
sanotaan, että luku
,
sanotaan, että luku 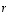 on lineaarikuvauksen
on lineaarikuvauksen 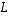 ominaisarvo
ominaisarvo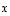 sen
ominaisvektori
sen
ominaisvektori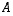 .
Yhtälöä
.
Yhtälöä 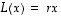 sanotaan
ominaisarvoyhtälöksi
sanotaan
ominaisarvoyhtälöksi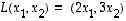 on ilmeisestikin jonkinlainen
on ilmeisestikin jonkinlainen 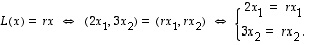
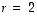 ja
ja 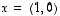 sekä toisaalta
sekä toisaalta 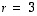 ja
ja 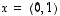 antavat ainakin eräät ominaisarvo- ja ominaisvektoriparit (ottamatta tässä vielä kantaa siihen, löytyykö mahdollisesti muitakin pareja).
antavat ainakin eräät ominaisarvo- ja ominaisvektoriparit (ottamatta tässä vielä kantaa siihen, löytyykö mahdollisesti muitakin pareja). 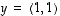 on
on 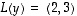 ja se ei siten ole enää vektorin
ja se ei siten ole enää vektorin 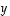 suuntainen. Tämä osoittaa, että ainakaan tämä vektori
suuntainen. Tämä osoittaa, että ainakaan tämä vektori 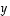 ei kelpaa ominaisvektoriksi.
ei kelpaa ominaisvektoriksi.
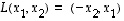 on vuorostaan
on vuorostaan 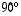
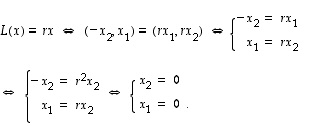
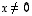 ,
että olisi
,
että olisi 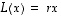 .
Tälle kuvaukselle ei siis ole olemassa ominaisarvoja eikä ominaisvektoreita.
.
Tälle kuvaukselle ei siis ole olemassa ominaisarvoja eikä ominaisvektoreita. 
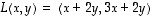 ominaisvektoreita:
ominaisvektoreita: 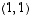 ,
,
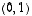 ,
,
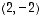 ,
,
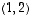 ,
,
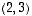 ,
,
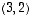 .
Myönteisessä tapauksessa ilmoita vastaava ominaisarvo.
.
Myönteisessä tapauksessa ilmoita vastaava ominaisarvo. esiintyvät tuntemattomina sekä ominaisarvo
esiintyvät tuntemattomina sekä ominaisarvo 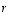 että ominaisvektori
että ominaisvektori 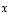 .
Kyseisessä yhtälöryhmässä on siten enemmän ratkaistavia muuttujia kuin yhtälöitä. Tällaisen yhtälöryhmän ratkaiseminen näyttäisi siten kovin epämääräiseltä. Seuraava tulos kuitenkin osoittaa, että mainituista tuntemattomista voidaan ensin ratkaista pelkästään ominaisarvot ilman ominaisvektoreiden laskemista. Ne voidaan laskea sitten jälkeenpäin.
.
Kyseisessä yhtälöryhmässä on siten enemmän ratkaistavia muuttujia kuin yhtälöitä. Tällaisen yhtälöryhmän ratkaiseminen näyttäisi siten kovin epämääräiseltä. Seuraava tulos kuitenkin osoittaa, että mainituista tuntemattomista voidaan ensin ratkaista pelkästään ominaisarvot ilman ominaisvektoreiden laskemista. Ne voidaan laskea sitten jälkeenpäin. 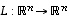 lineaarikuvaus ja
lineaarikuvaus ja 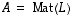 sitä vastaava neliömatriisi. Tällöin luku
sitä vastaava neliömatriisi. Tällöin luku 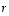 on kuvauksen
on kuvauksen 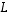 ominaisarvo, jos ja vain jos
ominaisarvo, jos ja vain jos 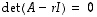 .
.
 on kuvauksen
on kuvauksen  ominaisarvo
ominaisarvo 
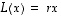 jollekin
jollekin 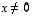
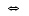
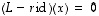 jollekin
jollekin 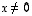
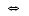
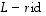 ei ole injektio
ei ole injektio 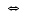
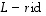 ei ole bijektio
ei ole bijektio 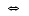
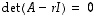 .
.

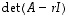 on kehityssäännöllä auki laskettuna todettavissa erääksi muuttujan
on kehityssäännöllä auki laskettuna todettavissa erääksi muuttujan 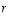 polynomiksi; se on yleistä muotoa
polynomiksi; se on yleistä muotoa 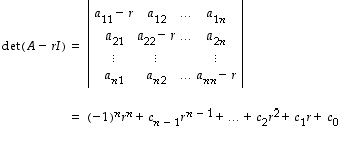
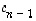 ,
...,
,
..., 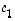 ,
,
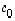 .
Se on nimeltään
.
Se on nimeltään 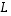 ja sitä vastaavan
ja sitä vastaavan 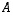 karakteristinen
karakteristinen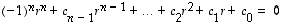
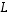 ja matriisin
ja matriisin 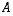
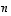 kappaletta, koska polynomi on
kappaletta, koska polynomi on 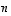 -asteinen. (Tässä viitataan siihen tosiasiaan, että
-asteinen. (Tässä viitataan siihen tosiasiaan, että 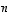 -asteisella reaalisella polynomilla on korkeintaan
-asteisella reaalisella polynomilla on korkeintaan 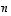 juurta.)
juurta.) 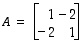
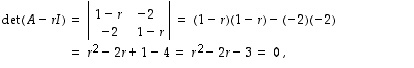
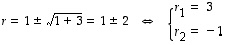 .
.
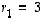 ,
ominaisvektorit saadaan ehdosta
,
ominaisvektorit saadaan ehdosta 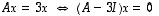 .
.

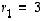 liittyvät ominaisvektorit ovat siis muotoa
liittyvät ominaisvektorit ovat siis muotoa 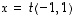 ,
missä
,
missä 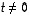 .
.
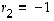 liittyvät ominaisvektorit:
liittyvät ominaisvektorit: 
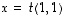 ,
missä
,
missä 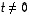 .
.

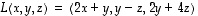 kaikki ominaisarvot ja ominaisarvoa
kaikki ominaisarvot ja ominaisarvoa 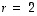 vastaavat ominaisvektorit.
vastaavat ominaisvektorit.