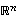karakterisoiva tulos.
Seurauslauseen 4.12 avulla saadaan seuraava avaruuksia 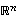karakterisoiva tulos.
Jokaisessa avaruuden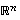 
kannassa on täsmälleen 
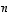vektoria.
Todistus.
Jos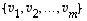 
on jokin avaruuden 
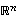kanta, seurauslauseen 4.12 kohdan (a) mukaan 
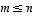ja toisaalta saman lauseen kohdan (b) mukaan 
.
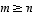Siis 
.
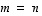Tämän lauseen mukaan kaikissa avaruuden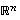 
kannoissa on täsmälleen 
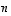vektoria. Tästä johtuen lukua 
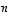sanotaan avaruuden 
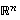dimensioksi eli
ulottuvuudeksi, merkitään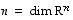 
.
Avaruutta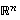 
sanotaan myös 
-
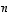ulotteiseksi. Suora 
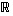on siis 1-ulotteinen, taso 
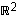on 2-ulotteinen, avaruus 
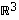on 3-ulotteinen jne.
Edellä olevat tulokset on muotoiltu vain koko avaruuksille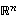 
.
Samat tulokset pätevät kuitenkin soveltaen kaikkiin näiden aliavaruuksiinkin. On vain ensin selvitettävä, mikä kyseisen aliavaruuden dimensio on eli montako lineaarisesti riippumatonta vektoria siitä on löydettävissä. Tässä luvussa pitäydytään kuitenkin vielä 'täysissä' avaruuksissa. Vasta luvussa 6 tarvitaan aliavaruuksien ulottuvuuksia.
Dimension kautta on nyt saatu aikaisemmin (pykälässä Virittäminen) kaivattu työtä helpottava lause.
Jokainen avaruuden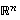 
lineaarisesti riippumaton vektorijoukko 
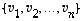on sen kanta.
Todistus.
Huomaa lauseen muotoilussa, että vektoreita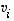 
on jo valmiiksi täsmälleen yhtä monta kuin mitä avaruuden dimensio on.
Jos nyt vektorijoukko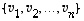 
ei olisikaan avaruuden 
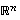kanta, se ei voisi virittää koko avaruutta. Lauseen 4.11 mukaan se voitaisiin täydentää kannaksi. Mutta silloin saataisin kanta, jossa olisi enemmän kuin 
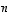vektoria. Tämä on ristiriidassa edellisen lauseen kanssa. Vektorijoukko 
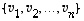muodostaa siis kannan.
Edellä olevalla lauseella on myös seuraava duaalinen tulos, jossa lineaarinen riippumattomuus korvataan virittämisellä. Näistä edellinen tulos on kuitenkin usein käytännöllisempi.
Jokainen avaruuden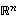 
virittävä vektorijoukko 
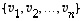on sen kanta.
Todistus.
Huomaa tämänkin lauseen muotoilussa, että vektoreita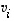 
on annettuna täsmälleen yhtä monta kuin mitä avaruuden dimensio on.
Riittää osoittaa, että annetut virittäjävektorit ovat lineaarisesti riippumattomat. Jos näin ei olisi, olisi jokin niistä toisten lineaarikombinaatio. Silloin tämä vektori voitaisiin korvata muilla kaikissa vektoreiden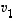 
,
,
..., 
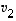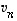lineaarikombinaatioissakin. Mutta koska nämä virittivät oletuksen mukaan koko avaruuden, saataisiin tulokseksi, että kaikki avaruuden 
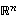vektorit virittyisivät jo 
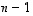vektorilla. Mutta se on ristiriidassa seurauslauseen 4.12 kohdan (b) kanssa. Niinpä vektorijoukon 
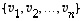on oltava lineaarisesti riippumaton ja siten kokonaisuudessaan myös kanta.
Usein kanta muodostetaan 'alhaalta ylöspäin': Ensin lähdetään jostain annetusta tai muutoin sopivasta vektorijoukosta, jonka vektoreita halutaan kantaan tulevan. Sitten tämä joukko 'puhdistetaan' lineaarisesti riippuvista vektoreista, ts. poistetaan tarvittaessa joukosta vektoreita niin kauan, että jäljelle jäävät vektorit ovat keskenään lineaarisesti riippumattomia. Jos näitä ei ole sen jälkeen tarpeeksi eli dimension verran, lisätään yksi vektori, joka ei ole näiden lineaarikombinaatio, jolloin se on näistä riippumaton. Tällä tavalla jatkaen lisätään joukkoon vektori kerrallaan, kunnes niitä on tarpeeksi paljon eli kunnes niitä on yhtä monta kuin dimension tiedetään olevan.
Tason vektorit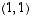 
,
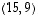ja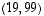 
ovat lineaarisesti riippuvat, sillä niitä on enemmän kuin avaruuden dimensio on (tässä 
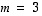ja 
,
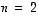ks. seurauksen 4.12 (a)-kohta). Jättämällä niistä yksi pois saadaan mahdollisesti aikaan kanta.
Muodostavatko sitten esimerkiksi vektorit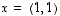 
ja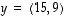 
tason kannan? Koska vektoreita on nyt kaksi ja tason dimensio on myös kaksi, riittää selvittää, ovatko ne lineaarisesti riippumattomat. Tämä taas näkyy heti, sillä 
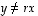millekään luvulle 
.
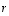Vastaus on siis myönteinen.
Lukija voi varmentua siitä, että muutkin kahden vektorin valinnat (kaksi mahdollisuutta) olisivat kelvanneet.
Avaruuden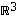 
vektorit 
,
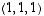ja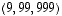 
eivät voi virittää sitä, sillä niitä on liian vähän (tässä 
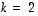ja 
,
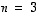ks. seurauksen 4.12 (b)-kohta). Lisäämällä yksikin, näistä kahdesta riippumaton vektori, saadaan kuitenkin kokoon jokin avaruuden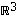 
kanta. Esimerkiksi vektori 
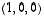kelpaa. Sitä varten riittää osoittaa, että valittu kolmikko muodostaa lineaarisesti riippumattoman vektorijoukon:
Myös kantavektorit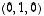 
ja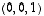 
olisivat olleet yhtä kelvollisia valintoja. Toki on olemassa loputtomasti muitakin valintamahdollisuuksia, mutta kantavektoreilla on usein helpointa toimia.
,
,
( 
)
,
,
( 
)
,
,
( 
)