Aliavaruuden ulottuvuus ja dimensiolause
Kuten luvussa 4 (pykälässä Ulottuvuus) osoitettiin avaruuksille, aliavaruuksillekin on samaan tapaan osoitettavissa, että niillä jokaisella on kantoja. Edelleen niiden jokaisessa kannassa on sama määrä vektoreita. Tätä määrää kutsutaan
aliavaruuden
dimensioksi.
Koska dimensio ilmoittaa lineaarisesti riippumattomien vektoreiden lukumäärän, on selvää, että aliavaruuden dimensio ei voi olla koskaan isompi kuin koko avaruuden dimensio. Edelleen pätee, että jos jonkin aliavaruuden dimensio on sama kuin koko avaruuden dimensio, se aliavaruus on itse asiassa välttämättä koko avaruus. Tämä tulos on seurausta lauseesta 4.14. Samaan tapaan nähdään, että jos kaksi aliavaruutta ovat sisäkkäisiä joukkoja, ei pienemmän aliavaruuden dimensio voi olla isompi kuin suuremman aliavaruuden dimensio. Lisäksi, jos tällaisten sisäkkäisten aliavaruuksien dimensiot ovat yhtä suuret, yhtyvät aliavaruudetkin.
Avaruudessa 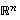 aliavaruuden dimensio voi kokonaislukuna siten olla vain jokin luvuista 0, 1, 2, ...,
aliavaruuden dimensio voi kokonaislukuna siten olla vain jokin luvuista 0, 1, 2, ..., 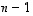 ,
,
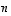 .
Tapauksessa 0 kyseessä on ns.
nolla-avaruus eli pelkän nollavektorin muodostama aliavaruus ja tapauksessa
.
Tapauksessa 0 kyseessä on ns.
nolla-avaruus eli pelkän nollavektorin muodostama aliavaruus ja tapauksessa 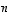 kyseessä on koko avaruus. Muissa tapauksissa kyseessä on ns.
aito
aliavaruus.
kyseessä on koko avaruus. Muissa tapauksissa kyseessä on ns.
aito
aliavaruus.
Esimerkki 6.13.
Selvitetään, millaisia voivat avaruuden 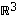 aliavaruudet olla. Koska koko avaruuden dimensio on kolme, voi sen aliavaruuden dimensio kokonaislukuna olla nolla, yksi, kaksi tai kolme. Lisäksi aliavaruudesta tiedetään, että se sisältää aina nollavektorin.
aliavaruudet olla. Koska koko avaruuden dimensio on kolme, voi sen aliavaruuden dimensio kokonaislukuna olla nolla, yksi, kaksi tai kolme. Lisäksi aliavaruudesta tiedetään, että se sisältää aina nollavektorin.
Jos dimensio on nolla tai kolme, kyseessä on ääritapaus, edellisessä nolla-avaruus eli pelkän nollavektorin muodostama aliavaruus ja jälkimmäisessä koko avaruus. Jos sitten aliavaruuden dimensio on yksi, se on yhden vektorin virittämä ja on siten joukkona jokin origon kautta kulkeva suora. Dimension ollessa kaksi aliavaruus on taas kahden lineaarisesti riippumattoman vektorin virittämä ja on silloin jokin origon kautta kulkeva taso. Aidot aliavaruudet ovat siten origon kautta kulkevat suorat ja tasot.

Lineaarikuvauksen 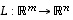 kuvajoukko
kuvajoukko 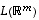 ja ydin
ja ydin 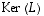 ovat molemmat aliavaruuksia eli joittenkin vektoreiden virittämiä, edellinen avaruudessa
ovat molemmat aliavaruuksia eli joittenkin vektoreiden virittämiä, edellinen avaruudessa 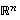 ja jälkimmäinen avaruudessa
ja jälkimmäinen avaruudessa 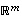 .
Ydin on määrittelynsä yhteydessä (pykälässä Ydin ja injektiivisyys) todettu aliavaruudeksi ja kuvajoukon osalta tämä jätetään harjoitustehtäväksi (tehtävä 7).
.
Ydin on määrittelynsä yhteydessä (pykälässä Ydin ja injektiivisyys) todettu aliavaruudeksi ja kuvajoukon osalta tämä jätetään harjoitustehtäväksi (tehtävä 7).
Kun käytetään lyhennettä
dim merkitsemään aliavaruuden suurinta lineaarisesti riippumattomien vektoreiden lukumäärää eli kyseisen aliavaruuden dimensiota, saadaan seuraava tärkeä tulos, ns. dimensiolause.
Lause 6.14. (Dimensiolause)
Lineaarikuvaukselle 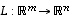 pätee aina, että
pätee aina, että
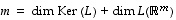 ,
,
ts. ytimessä ja kuvajoukossa on yhteensä yhtä monta riippumatonta vektoria kuin koko lähtöavaruudessa 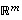 on.
on.
Todistus.
Olkoon kuvauksen 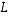 ydin vektoreiden
ydin vektoreiden 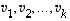 virittämä,
virittämä,
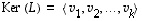 ,
,
missä vektorit 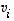 ovat lineaarisesti riippumattomia. Luku
ovat lineaarisesti riippumattomia. Luku 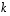 on silloin ytimen dimensio. Lisätään näihin vektoreihin jotkut vektorit
on silloin ytimen dimensio. Lisätään näihin vektoreihin jotkut vektorit 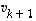 ,
...,
,
..., 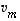 niin, että ne kaikki yhdessä muodostavat avaruuden
niin, että ne kaikki yhdessä muodostavat avaruuden 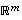 kannan. Lauseen 4.11 mukaan tämä on mahdollista.
kannan. Lauseen 4.11 mukaan tämä on mahdollista.
Mielivaltaiselle avaruuden 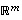 vektorille
vektorille 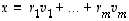 on nyt
on nyt
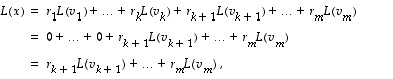
joten kuvajoukko 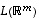 virittyy jo vektoreilla
virittyy jo vektoreilla 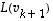 ,
...,
,
..., 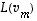 .
.
Osoitetaan, että nämä vektorit ovat lisäksi lineaarisesti riippumattomat. Jos
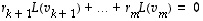 ,
,
lineaarisuuden perusteella on 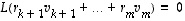 eli vektori
eli vektori 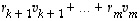 on ytimen
on ytimen 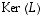 vektori. Koska ydin taas on vektorien
vektori. Koska ydin taas on vektorien 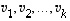 virittämä, on
virittämä, on
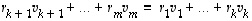
joillekin luvuille 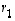 ,
...,
,
..., 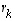 .
Vektorien
.
Vektorien 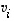 lineaarisen riippumattomuuden perusteella on kuitenkin oltava kaikkien kertoimien
lineaarisen riippumattomuuden perusteella on kuitenkin oltava kaikkien kertoimien 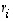 nollia. Erikoisesti silloin
nollia. Erikoisesti silloin 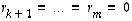 ,
mikä osoittaakin vektoreiden
,
mikä osoittaakin vektoreiden 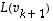 ,
...,
,
..., 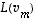 lineaarisen riippumattomuuden.
lineaarisen riippumattomuuden.
On siten todettu, että jos ytimen dimensio on 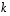 ,
kuvajoukon dimensio on
,
kuvajoukon dimensio on 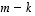 .
Yhteenlaskettuna ne antavat avaruuden
.
Yhteenlaskettuna ne antavat avaruuden 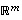 dimension
dimension 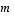 ,
kuten väitettiin.
,
kuten väitettiin.

Dimensiolauseen mukaan on voimassa yhtälö 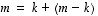 ,
missä
,
missä 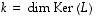 ja
ja 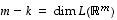 .
Kuvajoukko
.
Kuvajoukko 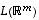 on avaruuden
on avaruuden 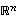 aliavaruus, joten lisäksi on voimassa ehto
aliavaruus, joten lisäksi on voimassa ehto 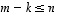 .
.
Esimerkki 6.19.
Kuvaus 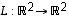 ,
,
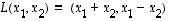 ,
on lineaarinen (totea se!). Lisäksi se on injektio (totea myös se!) ja sellaisena bijektio. Todetaan lisäksi laskemalla että sen käänteiskuvauksen lauseke on
,
on lineaarinen (totea se!). Lisäksi se on injektio (totea myös se!) ja sellaisena bijektio. Todetaan lisäksi laskemalla että sen käänteiskuvauksen lauseke on
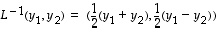 .
.
Asetetaan
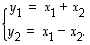
Tällöin
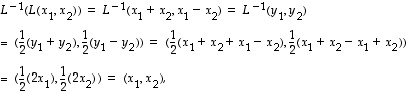
joten 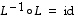 .
Vastaavasti todetaan, että myös
.
Vastaavasti todetaan, että myös 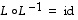 .
Siten
.
Siten 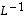 on todella kuvauksen
on todella kuvauksen 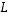 käänteiskuvaus.
käänteiskuvaus.
Saatu käänteiskuvaus voidaan myös todeta sen jälkeen helposti lineaariseksi, kun huomataan, että
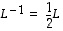 .
.
Tietysti myös lauseen 6.18 nojalla käänteiskuvaus on lineaarinen.

Opiskelutehtävä 22
Osoita, että lineaarikuvaus 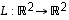 ,
,
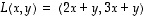 ,
,
on bijektio. Osoita lisäksi, että 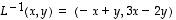 on sen käänteiskuvaus.
on sen käänteiskuvaus.
Vinkki tehtävään 22
Lineaariselle bijektiolle on siis 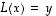 täsmälleen silloin kun
täsmälleen silloin kun 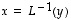 .
Yleisesti lineaaristen yhtälöiden ratkaisemisessa on seuraavan tuloksen periaate kätevä.
.
Yleisesti lineaaristen yhtälöiden ratkaisemisessa on seuraavan tuloksen periaate kätevä.
Esimerkki 6.21.
Esimerkin 6.15 lineaarikuvaukselle 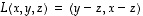 saatiin, että
saatiin, että 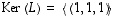 .
Tälle kuvaukselle yhtälön
.
Tälle kuvaukselle yhtälön
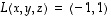
eli yhtälöryhmän
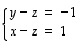
eräs ratkaisu on 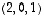 ,
mikä onkin helppo huomata. Siten sen kaikki ratkaisut ovat muotoa
,
mikä onkin helppo huomata. Siten sen kaikki ratkaisut ovat muotoa
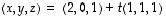 (
( 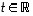 )
)
eli muotoa
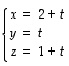 (
( 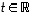 ).
).
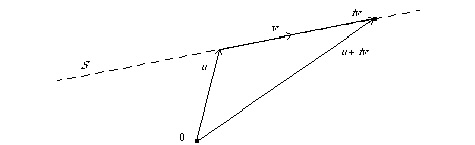
Geometrisesti ajatellen ratkaisut sijaitsevat pisteen 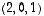 kautta kulkevalla ja vektorin
kautta kulkevalla ja vektorin 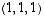 suuntaisella suoralla. Merkinnöin
suuntaisella suoralla. Merkinnöin 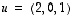 ja
ja 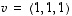 ratkaisujoukko on suora
ratkaisujoukko on suora 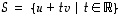 .
.

Havainnollistus: Lineaarikuvausten perustyyppejä
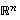 aliavaruuden dimensio voi kokonaislukuna siten olla vain jokin luvuista 0, 1, 2, ...,
aliavaruuden dimensio voi kokonaislukuna siten olla vain jokin luvuista 0, 1, 2, ..., 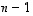 ,
,
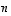 .
Tapauksessa 0 kyseessä on ns.
nolla-avaruus eli pelkän nollavektorin muodostama aliavaruus ja tapauksessa
.
Tapauksessa 0 kyseessä on ns.
nolla-avaruus eli pelkän nollavektorin muodostama aliavaruus ja tapauksessa 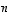 kyseessä on koko avaruus. Muissa tapauksissa kyseessä on ns.
aito
aliavaruus.
kyseessä on koko avaruus. Muissa tapauksissa kyseessä on ns.
aito
aliavaruus.  aliavaruudet olla. Koska koko avaruuden dimensio on kolme, voi sen aliavaruuden dimensio kokonaislukuna olla nolla, yksi, kaksi tai kolme. Lisäksi aliavaruudesta tiedetään, että se sisältää aina nollavektorin.
aliavaruudet olla. Koska koko avaruuden dimensio on kolme, voi sen aliavaruuden dimensio kokonaislukuna olla nolla, yksi, kaksi tai kolme. Lisäksi aliavaruudesta tiedetään, että se sisältää aina nollavektorin. 
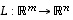
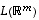 ja ydin
ja ydin 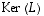 ovat molemmat
ovat molemmat 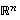 ja jälkimmäinen avaruudessa
ja jälkimmäinen avaruudessa 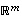 .
Ydin on määrittelynsä yhteydessä (pykälässä
.
Ydin on määrittelynsä yhteydessä (pykälässä 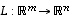 pätee aina, että
pätee aina, että 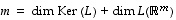 ,
,
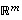 on.
on. 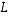 ydin vektoreiden
ydin vektoreiden 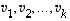 virittämä,
virittämä, 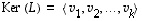 ,
,
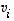 ovat lineaarisesti riippumattomia. Luku
ovat lineaarisesti riippumattomia. Luku 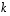 on silloin ytimen dimensio. Lisätään näihin vektoreihin jotkut vektorit
on silloin ytimen dimensio. Lisätään näihin vektoreihin jotkut vektorit 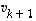 ,
...,
,
..., 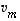 niin, että ne kaikki yhdessä muodostavat avaruuden
niin, että ne kaikki yhdessä muodostavat avaruuden 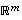 kannan. Lauseen
kannan. Lauseen  vektorille
vektorille 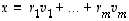 on nyt
on nyt 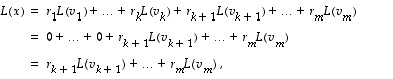
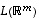 virittyy jo vektoreilla
virittyy jo vektoreilla 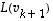 ,
...,
,
..., 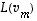 .
.
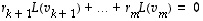 ,
,
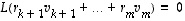 eli vektori
eli vektori 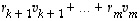 on ytimen
on ytimen 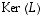 vektori. Koska ydin taas on vektorien
vektori. Koska ydin taas on vektorien 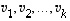 virittämä, on
virittämä, on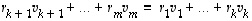
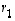 ,
...,
,
..., 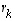 .
Vektorien
.
Vektorien 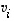 lineaarisen riippumattomuuden perusteella on kuitenkin oltava kaikkien kertoimien
lineaarisen riippumattomuuden perusteella on kuitenkin oltava kaikkien kertoimien 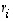 nollia. Erikoisesti silloin
nollia. Erikoisesti silloin 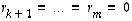 ,
mikä osoittaakin vektoreiden
,
mikä osoittaakin vektoreiden 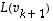 ,
...,
,
..., 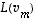 lineaarisen riippumattomuuden.
lineaarisen riippumattomuuden. 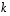 ,
kuvajoukon dimensio on
,
kuvajoukon dimensio on 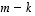 .
Yhteenlaskettuna ne antavat avaruuden
.
Yhteenlaskettuna ne antavat avaruuden 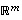 dimension
dimension 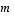 ,
kuten väitettiin.
,
kuten väitettiin. 
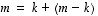 ,
missä
,
missä 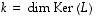 ja
ja 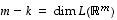 .
Kuvajoukko
.
Kuvajoukko 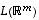 on avaruuden
on avaruuden 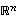 aliavaruus, joten lisäksi on voimassa ehto
aliavaruus, joten lisäksi on voimassa ehto 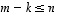 .
.
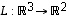 ,
,
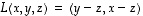 on lineaarinen (totea!). Määrätään sen ydin. Nyt
on lineaarinen (totea!). Määrätään sen ydin. Nyt 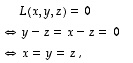
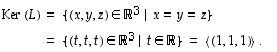
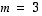 ja
ja 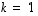 .
Kuva-avaruuden dimensio on näin ollen
.
Kuva-avaruuden dimensio on näin ollen 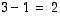 .
Koska se on sama kuin koko maaliavaruuden
.
Koska se on sama kuin koko maaliavaruuden 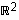 dimensio, kuvajoukko on koko avaruus eli kuvaus on surjektio. Esimerkiksi vektorit
dimensio, kuvajoukko on koko avaruus eli kuvaus on surjektio. Esimerkiksi vektorit 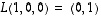 ja
ja 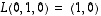 virittävät todella avaruuden
virittävät todella avaruuden 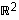 .
.

 lineaarikuvaus.
lineaarikuvaus.  ,
ei
,
ei  voi olla injektio.
voi olla injektio. 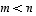 ,
ei
,
ei 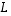 voi olla surjektio.
voi olla surjektio. 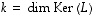 ,
jolloin dimensiolauseen mukaan
,
jolloin dimensiolauseen mukaan 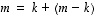 ,
missä
,
missä 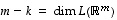 .
Lisäksi
.
Lisäksi 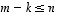 .
.
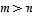 ,
on
,
on 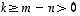 .
Siten
.
Siten 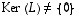 ja lauseen
ja lauseen 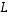 ei ole injektio.
ei ole injektio. 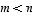 ,
on
,
on 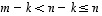 ,
joten
,
joten 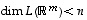 eli
eli 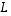 ei ole surjektio.
ei ole surjektio. 
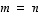 ). Jos sitten lineaarikuvaus toimii saman avaruuden sisällä, bijektiivisyyden osoittamiseksi ei tarvitsekaan käydä läpi surjektiivisuutta tai vaihtoehtoisesti injektiivisyyttä. Tämäkin on olennaisesti dimensiolauseen ansiota.
). Jos sitten lineaarikuvaus toimii saman avaruuden sisällä, bijektiivisyyden osoittamiseksi ei tarvitsekaan käydä läpi surjektiivisuutta tai vaihtoehtoisesti injektiivisyyttä. Tämäkin on olennaisesti dimensiolauseen ansiota. 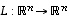 on bijektio, jos se on injektio tai jos se on surjektio.
on bijektio, jos se on injektio tai jos se on surjektio. 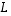 on injektio, on
on injektio, on 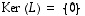 ja siis
ja siis 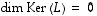 .
Dimensiolauseen mukaan on siten
.
Dimensiolauseen mukaan on siten 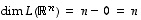 ,
joten kuvajoukon on oltava koko avaruus eli kuvauksen on oltava surjektionkin.
,
joten kuvajoukon on oltava koko avaruus eli kuvauksen on oltava surjektionkin. 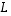 on surjektio, on
on surjektio, on 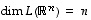 ,
jolloin dimensiolauseen mukaan
,
jolloin dimensiolauseen mukaan 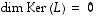 eli
eli 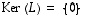 .
Kuvaus
.
Kuvaus 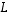 on siten injektiokin.
on siten injektiokin. 
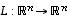 käänteiskuvaus
käänteiskuvaus 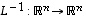 on myös lineaarinen.
on myös lineaarinen. 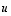 ja
ja 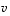 avaruuden
avaruuden 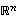 vektoreita. Surjektiivisuuden perusteella
vektoreita. Surjektiivisuuden perusteella 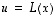 ja
ja 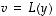 joillekin vektoreille
joillekin vektoreille 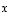 ja
ja 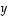 .
Silloin
.
Silloin 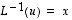 ja
ja 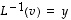 .
Lineaarisuuden perusteella taas
.
Lineaarisuuden perusteella taas 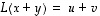 .
Siten
.
Siten 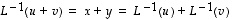 .
.
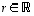 ,
on
,
on 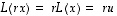 ,
ja siten
,
ja siten 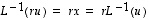 .
.
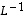 on siten lineaarinen.
on siten lineaarinen. 
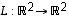 ,
,
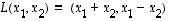 ,
on lineaarinen (totea se!). Lisäksi se on injektio (totea myös se!) ja sellaisena bijektio. Todetaan lisäksi laskemalla että sen käänteiskuvauksen lauseke on
,
on lineaarinen (totea se!). Lisäksi se on injektio (totea myös se!) ja sellaisena bijektio. Todetaan lisäksi laskemalla että sen käänteiskuvauksen lauseke on 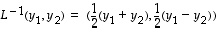 .
.
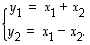
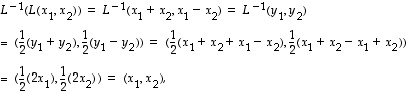
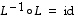 .
Vastaavasti todetaan, että myös
.
Vastaavasti todetaan, että myös 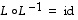 .
Siten
.
Siten 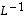 on todella kuvauksen
on todella kuvauksen 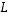 käänteiskuvaus.
käänteiskuvaus. 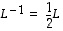 .
.

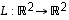 ,
,
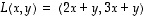 ,
,
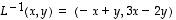 on sen käänteiskuvaus.
on sen käänteiskuvaus.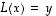 täsmälleen silloin kun
täsmälleen silloin kun 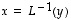 .
Yleisesti lineaaristen yhtälöiden ratkaisemisessa on seuraavan tuloksen periaate kätevä.
.
Yleisesti lineaaristen yhtälöiden ratkaisemisessa on seuraavan tuloksen periaate kätevä. 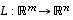 yhtälön
yhtälön 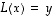 ratkaisut (silloin kun niitä on) ovat muotoa
ratkaisut (silloin kun niitä on) ovat muotoa 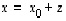 ,
missä
,
missä 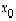 on jokin ko. yhtälön
on jokin ko. yhtälön 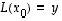 ja
ja 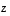 on yhtälön
on yhtälön 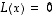 ratkaisu eli
ratkaisu eli 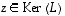 .
.
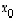 on jokin yksityisratkaisu ja
on jokin yksityisratkaisu ja 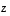 on yhtälön
on yhtälön 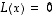 ratkaisu, on
ratkaisu, on 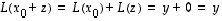 ,
,
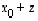 on eräs ratkaisu.
on eräs ratkaisu. 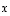 on ratkaisu, silloin on
on ratkaisu, silloin on 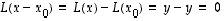 ,
,
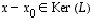 .
Siten jollekin ytimen vektorille
.
Siten jollekin ytimen vektorille 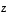 on
on 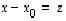 eli
eli 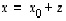 .
.

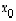 on yhtälön
on yhtälön 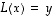 yksityisratkaisu
yksityisratkaisu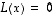 on yhtälöä
on yhtälöä 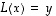 vastaava
homogeeninen
vastaava
homogeeninen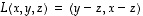 saatiin, että
saatiin, että 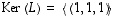 .
Tälle kuvaukselle yhtälön
.
Tälle kuvaukselle yhtälön 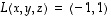
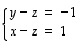
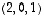 ,
mikä onkin helppo huomata. Siten sen kaikki ratkaisut ovat muotoa
,
mikä onkin helppo huomata. Siten sen kaikki ratkaisut ovat muotoa 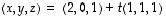 (
( 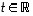 )
)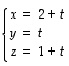 (
( 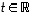 ).
). 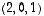 kautta kulkevalla ja vektorin
kautta kulkevalla ja vektorin 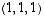 suuntaisella suoralla. Merkinnöin
suuntaisella suoralla. Merkinnöin 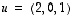 ja
ja 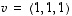 ratkaisujoukko on suora
ratkaisujoukko on suora 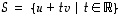 .
.