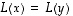 saadaan nimittäin, että
saadaan nimittäin, että 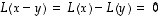 ,
ja kääntäen. Toisin sanoen vektoreiden
,
ja kääntäen. Toisin sanoen vektoreiden 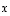 ja
ja 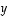 vertaaminen on yhtäpitävää vektorin
vertaaminen on yhtäpitävää vektorin 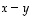 nollavektoriin vertaamisen kanssa. Yhtälön
nollavektoriin vertaamisen kanssa. Yhtälön 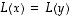 sijasta riittääkin siten tarkastella yhtälöä
sijasta riittääkin siten tarkastella yhtälöä 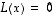 .
.
Lineaarikuvauksen injektiivisyyden tutkiminen voidaan siirtää origoon: ehdosta 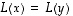 saadaan nimittäin, että
saadaan nimittäin, että 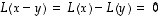 ,
ja kääntäen. Toisin sanoen vektoreiden
,
ja kääntäen. Toisin sanoen vektoreiden 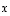 ja
ja 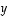 vertaaminen on yhtäpitävää vektorin
vertaaminen on yhtäpitävää vektorin 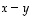 nollavektoriin vertaamisen kanssa. Yhtälön
nollavektoriin vertaamisen kanssa. Yhtälön 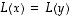 sijasta riittääkin siten tarkastella yhtälöä
sijasta riittääkin siten tarkastella yhtälöä 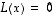 .
.
Määritellään, että lineaarikuvauksen 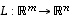 ydin on joukko
ydin on joukko
Kuvauksen 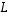 lineaarisuuden perusteella ytimen vektoreiden summat ja monikerrat ovat edelleen sen vektoreita, sillä jos
lineaarisuuden perusteella ytimen vektoreiden summat ja monikerrat ovat edelleen sen vektoreita, sillä jos 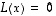 ja
ja 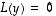 ,
niin myös
,
niin myös
Lineaarikuvauksen ydin on siis aina joidenkin vektorien virittämä aliavaruus. Seuraava tulos on jo oikeastaan edellä perusteltu, mutta todistetaan se vielä uudestaan.
Lineaarikuvaus 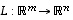 on injektio, jos ja vain jos
on injektio, jos ja vain jos 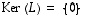 .
.
Todistus.
Jos 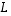 on injektio ja vektori
on injektio ja vektori 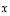 on ytimessä, on
on ytimessä, on 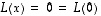 ,
joten injektiivisyyden perusteella
,
joten injektiivisyyden perusteella 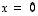 .
.
Jos taas ytimessä on vain nollavektori, ehdosta 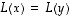 ja siitä, että
ja siitä, että
saadaan, että vektorin 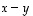 on oltava ytimen ainoa vektori, nollavektori, ts. saadaan, että
on oltava ytimen ainoa vektori, nollavektori, ts. saadaan, että 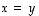 .
Kuvaus
.
Kuvaus 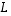 on siten injektio.
on siten injektio.
Opiskelutehtävän 20 perusteella tiedetään, että kuvaus 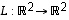 ,
,