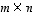 oleva matriisi on siis neliömatriisi täsmälleen silloin, kun
oleva matriisi on siis neliömatriisi täsmälleen silloin, kun 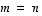 .
Seuraavassa on eräitä yleisesti käytettyjä nimityksiä neliömatriiseille
.
Seuraavassa on eräitä yleisesti käytettyjä nimityksiä neliömatriiseille 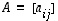 :
:
Sellaista matriisia, jossa on yhtä monta riviä kuin sarakettakin, sanotaan
neliömatriisiksi. Tyyppiä 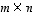 oleva matriisi on siis neliömatriisi täsmälleen silloin, kun
oleva matriisi on siis neliömatriisi täsmälleen silloin, kun 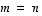 .
Seuraavassa on eräitä yleisesti käytettyjä nimityksiä neliömatriiseille
.
Seuraavassa on eräitä yleisesti käytettyjä nimityksiä neliömatriiseille 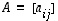 :
:
· Neliömatriisin 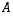 halkaisijalla olevat luvut
halkaisijalla olevat luvut 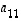 ,
,
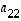 ,
...,
,
..., 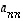 muodostavat sen
lävistäjän eli
diagonaalin.
muodostavat sen
lävistäjän eli
diagonaalin.
· Neliömatriisi on
lävistäjämatriisi eli
diagonaalimatriisi, jos lävistäjän ulkopuoliset luvut ovat nollia eli jos 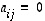 aina kun
aina kun 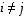 .
.
·
Yksikkömatriisi 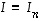 on sellainen diagonaalimatriisi, jonka kaikki diagonaalialkiot ovat ykkösiä. Ts. matriisi
on sellainen diagonaalimatriisi, jonka kaikki diagonaalialkiot ovat ykkösiä. Ts. matriisi  on yksikkömatriisi, jos
on yksikkömatriisi, jos 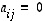 ,
aina kun
,
aina kun 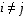 ,
ja jos
,
ja jos 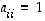 kaikilla
kaikilla 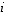 .
Yksikkömatriisia sanotaan myös
ykkösmatriisiksi tai
identtiseksi
matriisiksi.
Edellinen nimitys johtuu siitä, että se toimii matriisien kertolaskussa kuten luvuilla luku 1 (ks. lause 8.6), ja jälkimmäinen siitä, että se vastaa identtistä kuvausta.
.
Yksikkömatriisia sanotaan myös
ykkösmatriisiksi tai
identtiseksi
matriisiksi.
Edellinen nimitys johtuu siitä, että se toimii matriisien kertolaskussa kuten luvuilla luku 1 (ks. lause 8.6), ja jälkimmäinen siitä, että se vastaa identtistä kuvausta.
·
Kolmiomatriisi 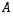 on sellainen neliömatriisi, jonka kaikki diagonaalin ala- tai yläpuoliset alkiot ovat nollia, ts.
on sellainen neliömatriisi, jonka kaikki diagonaalin ala- tai yläpuoliset alkiot ovat nollia, ts. 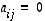 ,
aina kun
,
aina kun 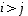 ,
jolloin kyseessä on tarkemmin sanottuna
yläkolmiomatriisi, tai aina kun
,
jolloin kyseessä on tarkemmin sanottuna
yläkolmiomatriisi, tai aina kun 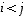 ,
jolloin kyseessä on
alakolmiomatriisi.
,
jolloin kyseessä on
alakolmiomatriisi.
Aikaisemmin lauseessa 6.18 on osoitettu, että lineaarisen bijektion käänteiskuvaus on myös bijektio. Selvitetään seuraavassa näiden kuvausten matriisivastaavuuksia.
Olkoon 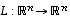 lineaarinen bijektio, jolloin siis sen käänteiskuvaus
lineaarinen bijektio, jolloin siis sen käänteiskuvaus 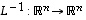 on myös lineaarinen. Kun sitten
on myös lineaarinen. Kun sitten 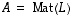 ja
ja 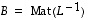 ovat näitä vastaavia matriiseja, ehdoista
ovat näitä vastaavia matriiseja, ehdoista
Tällainen matriisi 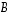 ,
joka toteuttaa viimeksi mainitut ehdot, on nimeltään matriisin
,
joka toteuttaa viimeksi mainitut ehdot, on nimeltään matriisin 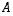 käänteismatriisi, merkitään
käänteismatriisi, merkitään 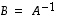 .
Tällöin sanotaan myös, että matriisi
.
Tällöin sanotaan myös, että matriisi 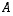 (ja siten myös
(ja siten myös 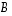 ) on
kääntyvä (eli
säännöllinen). Edellä annettu mielikuva vain yhden käänteismatriisin olemassaolosta on itse asiassa oikea, sillä jos myös matriisi
) on
kääntyvä (eli
säännöllinen). Edellä annettu mielikuva vain yhden käänteismatriisin olemassaolosta on itse asiassa oikea, sillä jos myös matriisi 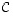 on matriisin
on matriisin 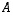 käänteismatriisi, saadaan ehdoista
käänteismatriisi, saadaan ehdoista 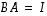 ja
ja 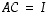 ,
että
,
että
Toisaalta sama seuraa myös siitä, että neliömatriisi on kääntyvä täsmälleen silloin, kun sitä vastaava lineaarikuvaus on bijektio, ja bijektion käänteiskuvaus taas on yksikäsitteinen kuvaus.
Yhteenvetona on saatu seuraava tulos.
Jos lineaarikuvaus 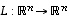 on bijektio ja sitä vastaa neliömatriisi
on bijektio ja sitä vastaa neliömatriisi 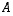 ,
on
,
on 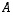 kääntyvä matriisi ja käänteiskuvausta
kääntyvä matriisi ja käänteiskuvausta 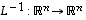 vastaa käänteismatriisi
vastaa käänteismatriisi 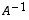 .
.
Määrittelyn mukaan käänteismatriisin pitää antaa sekä vasemmalta että oikealta kerrottuna tuloksi yksikkömatriisin. Oleellisesti dimensiolauseesta saadaan kuitenkin seuraava 'työnpuolituslause'.
Jos samankokoisille neliömatriiseille 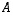 ja
ja 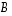 on
on 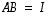 ,
on myös
,
on myös 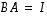 ,
ts. sekä
,
ts. sekä 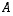 että
että 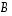 ovat kääntyviä ja toistensa käänteismatriiseja.
ovat kääntyviä ja toistensa käänteismatriiseja.
Todistus.
Olkoot 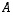 ja
ja 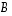 kokoa
kokoa 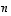 olevia neliömatriiseja, joille
olevia neliömatriiseja, joille 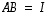 .
Olkoot edelleen
.
Olkoot edelleen 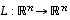 ja
ja 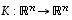 sellaisia lineaarikuvauksia, että
sellaisia lineaarikuvauksia, että 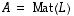 ja
ja 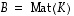 .
Ehdosta
.
Ehdosta 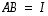 seuraa, että yhdistetty kuvaus
seuraa, että yhdistetty kuvaus 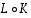 on identtinen kuvaus. Tällöin 'alla' oleva kuvaus
on identtinen kuvaus. Tällöin 'alla' oleva kuvaus 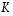 on välttämättä injektio (muutoin ei yhdistetty kuvauskaan voisi olla injektio) ja toisaalta 'päällä' oleva kuvaus
on välttämättä injektio (muutoin ei yhdistetty kuvauskaan voisi olla injektio) ja toisaalta 'päällä' oleva kuvaus 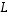 on surjektio (muutoin ei yhdistetty kuvauskaan voisi olla surjektio). Lauseen 6.17 perusteella kummatkin lineaarikuvaukset ovat siten bijektioita ja niillä molemmilla on edelleen käänteiskuvaukset.
on surjektio (muutoin ei yhdistetty kuvauskaan voisi olla surjektio). Lauseen 6.17 perusteella kummatkin lineaarikuvaukset ovat siten bijektioita ja niillä molemmilla on edelleen käänteiskuvaukset.
Osoitetaan seuraavaksi, että myös 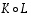 on identtinen kuvaus. Käyttäen sitä, että
on identtinen kuvaus. Käyttäen sitä, että 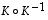 ja
ja 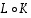 ovat identtisiä kuvauksia, voidaankin avaruuden
ovat identtisiä kuvauksia, voidaankin avaruuden 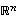 vektoreille
vektoreille 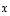 laskea seuraavasti:
laskea seuraavasti:
Siten 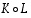 on todella identtinen kuvaus. Kuvauksia vastaaviin matriiseihin siirtymällä tästä tuloksesta seuraakin heti väitetty yhtälö
on todella identtinen kuvaus. Kuvauksia vastaaviin matriiseihin siirtymällä tästä tuloksesta seuraakin heti väitetty yhtälö 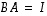 .
(Selvennöksenä todettakoon, että apuna käytetyt kuvaukset
.
(Selvennöksenä todettakoon, että apuna käytetyt kuvaukset 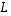 ja
ja 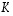 ovat näin itse asiassa osoittautuneet toistensa käänteiskuvauksiksi, ts.
ovat näin itse asiassa osoittautuneet toistensa käänteiskuvauksiksi, ts. 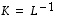 ja
ja 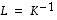 .
)
.
)
olemassa käänteismatriisia. Ensinnäkin 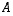 on neliömatriisi, joten sillä voi tyyppinsä puolesta olla käänteismatriisi. Jos sellainen on, se on samankokoinen kuin
on neliömatriisi, joten sillä voi tyyppinsä puolesta olla käänteismatriisi. Jos sellainen on, se on samankokoinen kuin 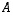 .
Etsitään siis sellaista
.
Etsitään siis sellaista 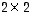 -matriisia
-matriisia 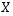 ,
että
,
että 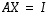 .
Ratkaistaan tämä matriisiyhtälö:
.
Ratkaistaan tämä matriisiyhtälö:
Käänteismatriisi on siis olemassa ja
Hyvä tarkistuskeino on todeta, että myös 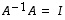 pätee.
pätee.
Pienikokoisen matriisin käänteismatriisin ratkaiseminen on mahdollista tehdä edellä kuvatulla tavalla, jossa käänteismatriisin 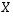 alkiot merkitään tuntemattomiksi muuttujiksi ja yhtälön
alkiot merkitään tuntemattomiksi muuttujiksi ja yhtälön 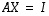 määräämät yhtälöryhmistä ratkaistaan kyseiset muuttujat. Gaussin ja Jordanin menetelmällä käänteismatriisin laskeminen onnistuu systemaattisemmin (ks. Käänteismatriisin laskeminen Gaussin ja Jordanin menetelmällä).
määräämät yhtälöryhmistä ratkaistaan kyseiset muuttujat. Gaussin ja Jordanin menetelmällä käänteismatriisin laskeminen onnistuu systemaattisemmin (ks. Käänteismatriisin laskeminen Gaussin ja Jordanin menetelmällä).
Seuraavassa on eräitä käänteismatriisin muodostamiseen liittyviä sääntöjä.
Jos 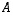 ja
ja 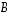 ovat samankokoisia kääntyviä neliömatriiseja ja luku
ovat samankokoisia kääntyviä neliömatriiseja ja luku 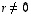 ,
on
,
on
Todistus.
Yleisesti matriisi 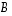 todistetaan helpoimmin matriisin
todistetaan helpoimmin matriisin 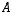 käänteismatriisiksi osoittamalla, että
käänteismatriisiksi osoittamalla, että 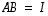 tai
tai 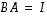 (toinen näistä riittää lauseen 8.8 mukaan). Todistetaan väitteet tämän periaatteen mukaisesti.
(toinen näistä riittää lauseen 8.8 mukaan). Todistetaan väitteet tämän periaatteen mukaisesti.
(a) Koska 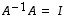 ,
on matriisin
,
on matriisin 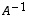 käänteismatriisi
käänteismatriisi 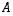 .
.
(c) Tämä väite seuraa nyt siitä, että
Lineaarisen yhtälön 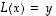 ratkaisujen muoto on todettu lauseessa 6.20. Matriiseille tulkittuna se ilmoittaa, että matriisiyhtälön
ratkaisujen muoto on todettu lauseessa 6.20. Matriiseille tulkittuna se ilmoittaa, että matriisiyhtälön 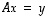 ratkaisut (silloin kun niitä on) ovat muotoa
ratkaisut (silloin kun niitä on) ovat muotoa 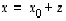 ,
missä ensinnäkin
,
missä ensinnäkin 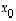 on jokin ko. yhtälön yksityisratkaisu, so.
on jokin ko. yhtälön yksityisratkaisu, so. 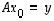 ,
ja toiseksi
,
ja toiseksi 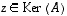 eli
eli 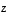 on (ns. homogeenisen) yhtälön
on (ns. homogeenisen) yhtälön 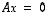 ratkaisu. Kääntyville matriiseille tämä tulos saadaan seuraavaan muotoon.
ratkaisu. Kääntyville matriiseille tämä tulos saadaan seuraavaan muotoon.
Jos tyyppiä 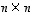 oleva neliömatriisi
oleva neliömatriisi 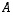 on kääntyvä, yhtälöllä
on kääntyvä, yhtälöllä 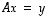 on jokaisella
on jokaisella 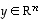 ratkaisuna
ratkaisuna 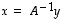 .
.
Todistus.
Jos 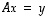 ,
voidaan päätellä seuraavasti
,
voidaan päätellä seuraavasti
Vektori 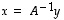 on siten ainoa mahdollinen ratkaisu. Jos taas valitaan
on siten ainoa mahdollinen ratkaisu. Jos taas valitaan 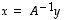 ,
saadaan, että
,
saadaan, että
on siis ratkaisuna 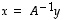 .
Käänteismatriisi
.
Käänteismatriisi 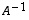 on laskettu esimerkissä 8.9, joten ratkaisuksi saadaan nyt
on laskettu esimerkissä 8.9, joten ratkaisuksi saadaan nyt