Determinantin ominaisuuksia
Eräs tärkeimmistä determinantin hyödyistä on sen antama kääntyvyysmittari matriiseille.
Lause 10.2.
Neliömatriisi  on kääntyvä, jos ja vain jos
on kääntyvä, jos ja vain jos 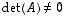 .
.
Todistus.
Esitetään tässä vain geometriseen havaintoon perustuva päättely ohittaen tarkan matemaattisen muotoilun. Algebrallisempi perustelu löytyy esimerkiksi Kahanpään ja Hannukaisen luentomonisteesta (pykälä 2.5).
Luvun 7 perusteella tiedetään, että neliömatriisi 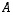 on kääntyvä, jos ja vain jos sitä vastaava lineaarikuvaus
on kääntyvä, jos ja vain jos sitä vastaava lineaarikuvaus 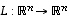 on bijektio, mihin toisaalta lauseen 6.17 mukaan riittää sen surjektiivisuus. Tämä on taas yhtäpitävää sen kanssa, että matriisin
on bijektio, mihin toisaalta lauseen 6.17 mukaan riittää sen surjektiivisuus. Tämä on taas yhtäpitävää sen kanssa, että matriisin 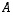 sarakevektorit virittävät koko avaruuden
sarakevektorit virittävät koko avaruuden 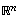 ,
ja se edelleen sen kanssa, että nämä vektorit eivät viritä surkastunutta suuntaissärmiötä eli särmiötä, jonka tilavuus on nolla. Suuntaissärmiön tilavuus taas on sen virittävien vektoreiden determinantin itseisarvo. Kaikki mainitut yhtäpitävyyspäättelyt yhdistämällä saadaan väite.
,
ja se edelleen sen kanssa, että nämä vektorit eivät viritä surkastunutta suuntaissärmiötä eli särmiötä, jonka tilavuus on nolla. Suuntaissärmiön tilavuus taas on sen virittävien vektoreiden determinantin itseisarvo. Kaikki mainitut yhtäpitävyyspäättelyt yhdistämällä saadaan väite.

Yllä olevan mukaan yleinen 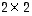 -matriisi
-matriisi
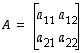
on kääntyvä täsmälleen silloin, kun
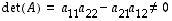 .
.
Tällä ehdolla sen käänteismatriisi on
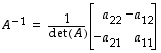 ,
,
mikä on helppo tarkistaa laskemalla. Tämän säännön mukaisesti 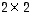 -matriisin käänteismatriisi on siten helppo muodostaa. Mitään yhtä yksinkertaista sääntöä ei valitettavasti ole olemassa isompikokoisille matriiseille.
-matriisin käänteismatriisi on siten helppo muodostaa. Mitään yhtä yksinkertaista sääntöä ei valitettavasti ole olemassa isompikokoisille matriiseille.
Seuraavissa lauseissa on eräitä determinanttia koskevia laskusääntöjä.
Lause 10.3.
Nollamatriisin determinantti on nolla ja yksikkömatriisin yksi. Yleisemmin diagonaalimatriisin determinantti on lävistäjäalkioiden tulo.
Todistus.
Ensinnäkin 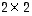 -diagonaalimatriisin determinantti on yksinkertaisesti lävistäjäalkioiden tulo. Kehittämissäännöstä nähdään toisaalta heti, että isompaa kokoa olevan matriisin determinantti on sen paikassa (1,1) olevan alkion ja sen suhteen muodostetun alideterminantin tulo (sillä kehittämissäännössä muut summattavat ovat nollia). Tämän perusteella se ominaisuus, että diagonaalimatriisin determinantti on lävistäjäalkioiden tulo, periytyy
-diagonaalimatriisin determinantti on yksinkertaisesti lävistäjäalkioiden tulo. Kehittämissäännöstä nähdään toisaalta heti, että isompaa kokoa olevan matriisin determinantti on sen paikassa (1,1) olevan alkion ja sen suhteen muodostetun alideterminantin tulo (sillä kehittämissäännössä muut summattavat ovat nollia). Tämän perusteella se ominaisuus, että diagonaalimatriisin determinantti on lävistäjäalkioiden tulo, periytyy 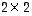 -diagonaalimatriiseilta kaiken kokoisille diagonaalimatriiseille.
-diagonaalimatriiseilta kaiken kokoisille diagonaalimatriiseille.
Nollamatriisin ja yksikkömatriisin determinantit saadaan tästä erikoistapauksena.

Lause 10.4.
Tyyppiä 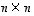 oleville neliömatriiseille
oleville neliömatriiseille 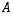 ja
ja 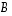 pätevät seuraavat:
pätevät seuraavat:
(1) 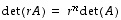 kaikille
kaikille 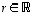 ,
,
(2) 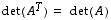 ,
,
(3) 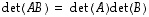 ,
,
(4) jos matriisi 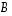 on kääntyvä, on
on kääntyvä, on
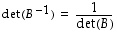 ,
,
(5) jos matriisi 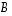 on kääntyvä ja
on kääntyvä ja  ,
on
,
on 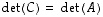 .
.
Todistus.
(1) Väite seuraa siitä, että matriisin 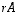 determinanttia laskettaessa luku
determinanttia laskettaessa luku 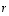 voidaan determinantin kehityssääntöä toistuvasti käytettäessä ottaa joka kerta tekijäksi. Viimeisessä vaiheessa,
voidaan determinantin kehityssääntöä toistuvasti käytettäessä ottaa joka kerta tekijäksi. Viimeisessä vaiheessa, 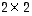 -alideterminantteja laskettaessa, luku
-alideterminantteja laskettaessa, luku 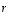 voidaan ottaa kahdesti tekijäksi ja jäljelle jäävät matriisiin
voidaan ottaa kahdesti tekijäksi ja jäljelle jäävät matriisiin 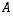 liittyvät alideterminantit. Yhteensä luku
liittyvät alideterminantit. Yhteensä luku 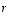 voidaan ottaa tekijäksi täsmälleen
voidaan ottaa tekijäksi täsmälleen 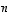 kertaa.
kertaa.
(2) - (3) Näiden kahden kohdan väitteet voidaan periaatteessa todistaa suoralla laskulla, mutta se lienee ylivoimaisen pitkä tapa. Todistusta voidaan lyhentää oleellisesti ottamalla käyttöön sopivia työkaluja (alternoivien multilineaarikuvausten teoriasta). Ohitetaan todistukset kuitenkin tässä ja viitataan näiden osalta Kahanpään ja Hannukaisen luentomonisteeseen (pykälä 2.4).
(4) Koska 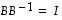 ,
on
,
on 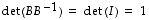 .
Siten edellisen kohdan perusteella on
.
Siten edellisen kohdan perusteella on 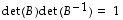 ,
mistä saadaan väite.
,
mistä saadaan väite.
(5) Kahden edellisen kohdan perusteella on
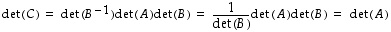 .
.

Edellä olevan lauseen viimeisen kohdan eli kohdan (5) perusteella lineaarikuvausta ennen kannanvaihtoa ja sen jälkeen vastaavien matriisien (ks. lause 9.4) determinantit ovat aina samat. Voidaan siis sopia, että
lineaarikuvauksen 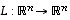 determinantti on minkä tahansa sitä vastaavan matriisin
determinantti on minkä tahansa sitä vastaavan matriisin 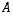 determinantti. Geometrisesti tämän determinantin itseisarvo ilmoittaa, missä suhteessa suunnikkaiden pinta-alat (kun
determinantti. Geometrisesti tämän determinantin itseisarvo ilmoittaa, missä suhteessa suunnikkaiden pinta-alat (kun 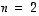 ) tai suuntaissärmiöiden tilavuudet (kun
) tai suuntaissärmiöiden tilavuudet (kun 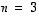 ) tai yleistettyjen suuntaissärmiöiden mitat (kun
) tai yleistettyjen suuntaissärmiöiden mitat (kun 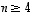 ) muuttuvat kuvauksessa.
) muuttuvat kuvauksessa.
Opiskelutehtävä 39
(a) Varmenna lauseen 10.4 kohdan (2) toimivuus matriisille
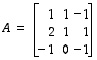 .
.
(b) Varmenna lauseen 10.4 kohdan (3) toimivuus matriiseille
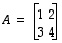
ja
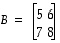 .
.
(c) Varmenna lauseen 10.4 kohdan (4) toimivuus (a)-kohdan matriisille 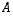 .
(Huomaa, että
.
(Huomaa, että 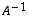 on laskettu esimerkissä 8.13)
on laskettu esimerkissä 8.13)
Vinkki tehtävään 39
 on kääntyvä, jos ja vain jos
on kääntyvä, jos ja vain jos 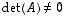 .
.
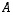 on kääntyvä, jos ja vain jos sitä vastaava lineaarikuvaus
on kääntyvä, jos ja vain jos sitä vastaava lineaarikuvaus 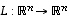 on bijektio, mihin toisaalta lauseen 6.17 mukaan riittää sen surjektiivisuus. Tämä on taas yhtäpitävää sen kanssa, että matriisin
on bijektio, mihin toisaalta lauseen 6.17 mukaan riittää sen surjektiivisuus. Tämä on taas yhtäpitävää sen kanssa, että matriisin 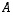 sarakevektorit virittävät koko avaruuden
sarakevektorit virittävät koko avaruuden 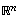 ,
ja se edelleen sen kanssa, että nämä vektorit eivät viritä surkastunutta suuntaissärmiötä eli särmiötä, jonka tilavuus on nolla. Suuntaissärmiön tilavuus taas on sen virittävien vektoreiden determinantin itseisarvo. Kaikki mainitut yhtäpitävyyspäättelyt yhdistämällä saadaan väite.
,
ja se edelleen sen kanssa, että nämä vektorit eivät viritä surkastunutta suuntaissärmiötä eli särmiötä, jonka tilavuus on nolla. Suuntaissärmiön tilavuus taas on sen virittävien vektoreiden determinantin itseisarvo. Kaikki mainitut yhtäpitävyyspäättelyt yhdistämällä saadaan väite. 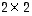 -matriisi
-matriisi 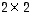 -matriisin käänteismatriisi on siten helppo muodostaa. Mitään yhtä yksinkertaista sääntöä ei valitettavasti ole olemassa isompikokoisille matriiseille.
-matriisin käänteismatriisi on siten helppo muodostaa. Mitään yhtä yksinkertaista sääntöä ei valitettavasti ole olemassa isompikokoisille matriiseille. 
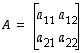
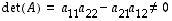 .
.
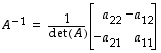 ,
,
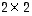 -diagonaalimatriisin determinantti on yksinkertaisesti lävistäjäalkioiden tulo. Kehittämissäännöstä nähdään toisaalta heti, että isompaa kokoa olevan matriisin determinantti on sen paikassa (1,1) olevan alkion ja sen suhteen muodostetun alideterminantin tulo (sillä kehittämissäännössä muut summattavat ovat nollia). Tämän perusteella se ominaisuus, että diagonaalimatriisin determinantti on lävistäjäalkioiden tulo, periytyy
-diagonaalimatriisin determinantti on yksinkertaisesti lävistäjäalkioiden tulo. Kehittämissäännöstä nähdään toisaalta heti, että isompaa kokoa olevan matriisin determinantti on sen paikassa (1,1) olevan alkion ja sen suhteen muodostetun alideterminantin tulo (sillä kehittämissäännössä muut summattavat ovat nollia). Tämän perusteella se ominaisuus, että diagonaalimatriisin determinantti on lävistäjäalkioiden tulo, periytyy 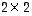 -diagonaalimatriiseilta kaiken kokoisille diagonaalimatriiseille.
-diagonaalimatriiseilta kaiken kokoisille diagonaalimatriiseille. 
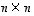 oleville neliömatriiseille
oleville neliömatriiseille 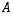 ja
ja 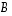 pätevät seuraavat:
pätevät seuraavat: 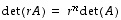 kaikille
kaikille 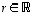 ,
,
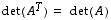 ,
,
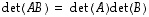 ,
,
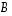 on
on 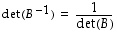 ,
,
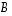 on kääntyvä ja
on kääntyvä ja  ,
on
,
on 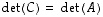 .
.
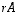 determinanttia laskettaessa luku
determinanttia laskettaessa luku 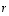 voidaan determinantin kehityssääntöä toistuvasti käytettäessä ottaa joka kerta tekijäksi. Viimeisessä vaiheessa,
voidaan determinantin kehityssääntöä toistuvasti käytettäessä ottaa joka kerta tekijäksi. Viimeisessä vaiheessa, 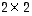 -alideterminantteja laskettaessa, luku
-alideterminantteja laskettaessa, luku 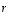 voidaan ottaa kahdesti tekijäksi ja jäljelle jäävät matriisiin
voidaan ottaa kahdesti tekijäksi ja jäljelle jäävät matriisiin 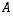 liittyvät alideterminantit. Yhteensä luku
liittyvät alideterminantit. Yhteensä luku 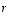 voidaan ottaa tekijäksi täsmälleen
voidaan ottaa tekijäksi täsmälleen 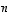 kertaa.
kertaa. 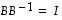 ,
on
,
on 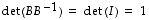 .
Siten edellisen kohdan perusteella on
.
Siten edellisen kohdan perusteella on 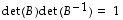 ,
mistä saadaan väite.
,
mistä saadaan väite. 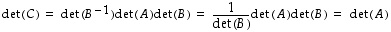 .
.

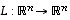 determinantti
determinantti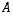 determinantti. Geometrisesti tämän determinantin itseisarvo ilmoittaa, missä suhteessa suunnikkaiden pinta-
determinantti. Geometrisesti tämän determinantin itseisarvo ilmoittaa, missä suhteessa suunnikkaiden pinta-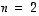 ) tai suuntaissärmiöiden
) tai suuntaissärmiöiden 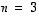 ) tai yleistettyjen suuntaissärmiöiden
) tai yleistettyjen suuntaissärmiöiden 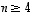 ) muuttuvat kuvauksessa.
) muuttuvat kuvauksessa. 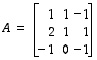 .
.
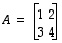
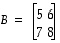 .
.
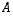 .
(Huomaa, että
.
(Huomaa, että 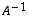 on laskettu esimerkissä
on laskettu esimerkissä