Esimerkki 9.1.
Tiedetään, että tason vektorit 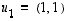 ja
ja 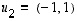 kelpaavat sen kannaksi. Miten saadaan laskettua jonkin vektorin koordinaatit tässä kannassa?
kelpaavat sen kannaksi. Miten saadaan laskettua jonkin vektorin koordinaatit tässä kannassa?
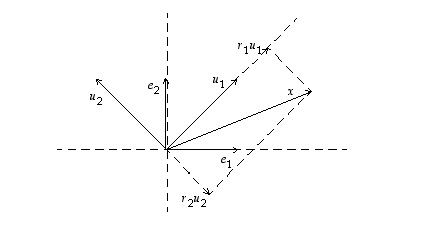
Olkoon vastauksen löytämistä varten 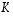 se tason lineaarikuvaus (ns. kannanvaihto), jolle
se tason lineaarikuvaus (ns. kannanvaihto), jolle 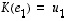 ja
ja 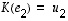 .
Sitä vastaava matriisi on
.
Sitä vastaava matriisi on
ja sen yleinen lauseke on muotoa
Lasketaan seuraavaksi käänteismatriisi 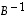 (kuvauksen kääntyvyys on nimittäin ilmeistä). Kaaviomuunnoksesta
(kuvauksen kääntyvyys on nimittäin ilmeistä). Kaaviomuunnoksesta
ja siten käänteiskuvauksen 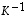 lauseke on
lauseke on
ts. jos 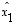 ja
ja 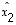 ovat vektorin
ovat vektorin 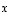 koordinaatit kannassa
koordinaatit kannassa 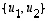 ,
on
,
on
Muuttujat toisinpäin ratkaistuna tämä on yhtäpitävää sen kanssa, että
Esimerkiksi konkreettiselle vektorille 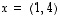 saadaan tämän mukaan, että
saadaan tämän mukaan, että
ts. vektorin 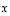 koordinaatit kannassa
koordinaatit kannassa 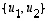 ovat 5/2 ja 3/2.
ovat 5/2 ja 3/2.
Yleistetään seuraavaksi tilanne avaruuteen 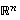 .
Tulos on nyt seuraavanlainen. Sen todistus menee kuten edellä, vektorit vain ovat nyt monikomponenttisia ja matriisit isompia kooltaan.
.
Tulos on nyt seuraavanlainen. Sen todistus menee kuten edellä, vektorit vain ovat nyt monikomponenttisia ja matriisit isompia kooltaan.
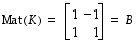
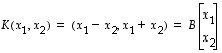 .
.

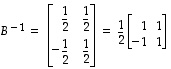
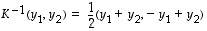 .
.
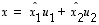 ,
,
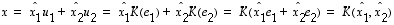
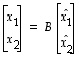 .
.
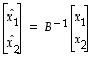 .
.
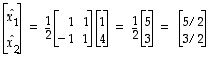 ,
,
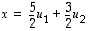 ,
,

 avaruuden
avaruuden  luonnollinen kanta (tai yleisemmin jokin entinen kanta) ja
luonnollinen kanta (tai yleisemmin jokin entinen kanta) ja 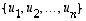 sen jokin toinen kanta (uusi kanta). Olkoon edelleen
sen jokin toinen kanta (uusi kanta). Olkoon edelleen 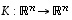 se yksikäsitteisesti määrätty lineaarikuvaus, joka kuvaa kunkin kantavektorin
se yksikäsitteisesti määrätty lineaarikuvaus, joka kuvaa kunkin kantavektorin 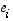 vastaavaksi kantavektoriksi
vastaavaksi kantavektoriksi 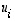 ,
eli on ns.
kannanvaihtokuvaus
,
eli on ns.
kannanvaihtokuvaus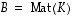
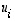 (tai tarkemmin niiden koordinaatit kannassa
(tai tarkemmin niiden koordinaatit kannassa 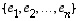 ). Tällöin avaruuden
). Tällöin avaruuden 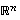 vektorin
vektorin 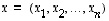 koordinaatit
koordinaatit 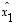 ,
,
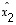 ,
...,
,
..., 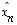 kannassa
kannassa 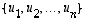 saadaan kaavasta
saadaan kaavasta 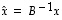
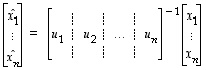 .
.
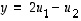 .
Mikä vektori
.
Mikä vektori 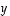 on eli mitkä ovat sen koordinaatit luonnollisessa kannassa? Koska sen koordinaatit kannassa
on eli mitkä ovat sen koordinaatit luonnollisessa kannassa? Koska sen koordinaatit kannassa 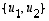 ovat
ovat 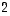 ja
ja 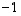 ,
saadaan, että
,
saadaan, että 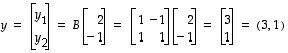 .
.
 koordinaatit luonnollisessa kannassa ovat siten
koordinaatit luonnollisessa kannassa ovat siten 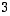 ja
ja 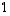 .
Toisaalta tietenkin suoraan voidaan laskea, että
.
Toisaalta tietenkin suoraan voidaan laskea, että 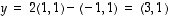 .
.
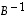 on laskettu esimerkissä
on laskettu esimerkissä  .
.
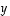 koordinaatit kannassa
koordinaatit kannassa 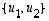 ovat
ovat 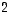 ja
ja 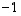 ,
kuten annettiinkin.
,
kuten annettiinkin. 
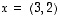 ja
ja 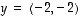 kannassa
kannassa 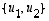 ,
missä
,
missä 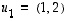 ja
ja 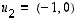 .
Tee se sekä graafisesti päätellen että laskien. Mieti jälkimmäisessä, miten voit hyödyntää kannanvaihtokuvausta luonnollisesta kannasta
.
Tee se sekä graafisesti päätellen että laskien. Mieti jälkimmäisessä, miten voit hyödyntää kannanvaihtokuvausta luonnollisesta kannasta 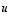 -kantaan.
-kantaan. 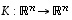 kannanvaihto
kannanvaihto 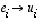 ja
ja 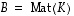 .
Tarkastellaan nyt tämän lisäksi lineaarikuvausta
.
Tarkastellaan nyt tämän lisäksi lineaarikuvausta 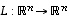 ,
jota luonnollisessa kannassa vastatkoon matriisi
,
jota luonnollisessa kannassa vastatkoon matriisi 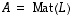 .
Mikä on silloin kuvausta
.
Mikä on silloin kuvausta  vastaava matriisi kannassa
vastaava matriisi kannassa 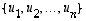 ? (Se ei ole tietenkään
? (Se ei ole tietenkään 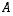 !)
!) 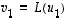 eli matriisimerkinnöin
eli matriisimerkinnöin 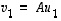 .
Tämän vektorin koordinaatit kannassa
.
Tämän vektorin koordinaatit kannassa 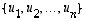 saadaan yllä olevan mukaisesti kaavasta
saadaan yllä olevan mukaisesti kaavasta 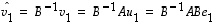 .
.
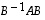 ensimmäinen sarake. Aivan vastaavasti voidaan yleisemmin nähdä, että vektorien
ensimmäinen sarake. Aivan vastaavasti voidaan yleisemmin nähdä, että vektorien 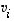 koordinaatit kannassa
koordinaatit kannassa 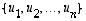 saadaan kaavasta
saadaan kaavasta 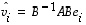 .
.
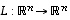 vastaa kannassa
vastaa kannassa 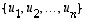 matriisi
matriisi 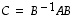 .
.
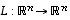 vastaa entisessä kannassa
vastaa entisessä kannassa 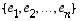 matriisi
matriisi 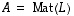 ,
uudessa kannassa
,
uudessa kannassa 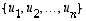 sitä vastaa matriisi
sitä vastaa matriisi 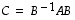 ,
,
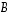 on kannanvaihtoa entisestä kannasta uuteen kantaan (entisessä kannassa) vastaava matriisi.
on kannanvaihtoa entisestä kannasta uuteen kantaan (entisessä kannassa) vastaava matriisi. 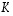 ja sitä vastaavan matriisin
ja sitä vastaavan matriisin 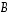 lisäksi annettu lineaarikuvaus
lisäksi annettu lineaarikuvaus 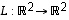 ,
,
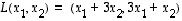 ,
jolloin
,
jolloin 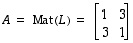 .
.
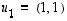 ja
ja 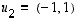 muodostamassa kannassa kuvausta
muodostamassa kannassa kuvausta 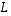 vastaa silloin matriisi
vastaa silloin matriisi 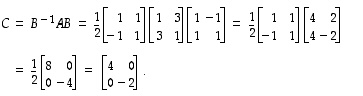
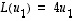 ja
ja 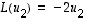 .
Siten on sattumalta löydetty kaksi suuntaa, joissa kuvaus
.
Siten on sattumalta löydetty kaksi suuntaa, joissa kuvaus 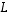 vain venyttää vektoreita (vaihtaen tosin lisäksi toisessa tapauksessa suunnan päinvastaiseksi). Myöhemmin ominaisarvoprobleeman yhteydessä (luvussa
vain venyttää vektoreita (vaihtaen tosin lisäksi toisessa tapauksessa suunnan päinvastaiseksi). Myöhemmin ominaisarvoprobleeman yhteydessä (luvussa 
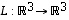 ,
,
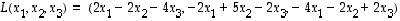 ,
,
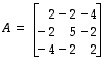 .
.
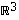 kantaa
kantaa 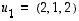 ,
,
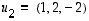 ja
ja 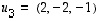 vastaavan kannanvaihdon matriisi taasen on
vastaavan kannanvaihdon matriisi taasen on 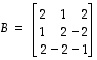 .
.
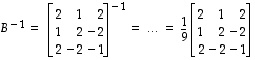 .
.
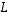 vastaa kannassa
vastaa kannassa 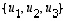 matriisi
matriisi 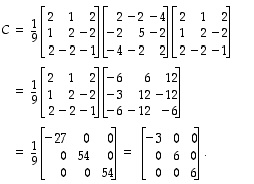
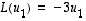 ,
,
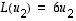 ja
ja 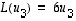 .
Taasen saatiin tulokseksi samalla tavalla erikoinen tilanne kuin edellisessä esimerkissä!
.
Taasen saatiin tulokseksi samalla tavalla erikoinen tilanne kuin edellisessä esimerkissä! 
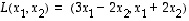
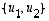 .
.