Käänteismatriisin laskeminen Gaussin ja Jordanin menetelmällä
Gaussin ja Jordanin algoritmia (ks. luku 3) voidaan käyttää myös käänteismatriisin laskemiseen. Menettelyn esittämistä varten olkoon 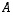 kokoa
kokoa 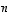 oleva neliömatriisi, jolle käänteismatriisia pyritään etsimään. Merkitään sitä varten muodostetussa yhtälössä
oleva neliömatriisi, jolle käänteismatriisia pyritään etsimään. Merkitään sitä varten muodostetussa yhtälössä 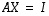 matriisin
matriisin 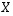 sarakkeita vektoreilla
sarakkeita vektoreilla 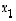 ,
,
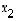 ,
...,
,
..., 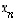 .
Yksikkömatriisin
.
Yksikkömatriisin 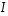 sarakkeet muodostuvat taas kantavektoreista
sarakkeet muodostuvat taas kantavektoreista 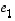 ,
,
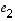 ,
...,
,
..., 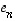 .
Kun matriisilla
.
Kun matriisilla 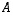 kerrotaan matriisin
kerrotaan matriisin 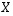 jokin sarake, tulokseksi saadaan tulon
jokin sarake, tulokseksi saadaan tulon 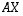 vastaava sarake. Siten matriisiyhtälön
vastaava sarake. Siten matriisiyhtälön 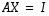 ratkaiseminen on yhtäpitävää vektoriyhtälöiden
ratkaiseminen on yhtäpitävää vektoriyhtälöiden 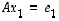 ,
,
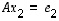 ,
...,
,
..., 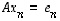 ratkaisemisen kanssa.
ratkaisemisen kanssa.
Matriisiyhtälön 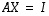 ratkaiseminen voidaan näin ollen tehdä sarakkeittain ja tehtävä voidaan siten periaatteessa paloitella
ratkaiseminen voidaan näin ollen tehdä sarakkeittain ja tehtävä voidaan siten periaatteessa paloitella 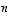 yhtälön ratkaisemiseen. Algoritmisesti nämä yhtälöt voidaan kuitenkin ratkaista yhtäaikaisesti. Jokaisen yhtälön ratkaisemisessahan kerroinmatriisi on aina sama ja siten sen muokkaaminen yksinkertaisempaan muotoon voidaan ajatella tehtävän joka kerta samalla tavalla. Kokonaisuudessaan ideana onkin nyt siis pyrkiä kaaviosta
yhtälön ratkaisemiseen. Algoritmisesti nämä yhtälöt voidaan kuitenkin ratkaista yhtäaikaisesti. Jokaisen yhtälön ratkaisemisessahan kerroinmatriisi on aina sama ja siten sen muokkaaminen yksinkertaisempaan muotoon voidaan ajatella tehtävän joka kerta samalla tavalla. Kokonaisuudessaan ideana onkin nyt siis pyrkiä kaaviosta 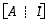 muotoa
muotoa 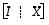 olevaan kaavioon, josta silloin käänteismatriisi
olevaan kaavioon, josta silloin käänteismatriisi 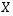 voitaisiin lukea.
voitaisiin lukea.
Esimerkki 8.13.
Etsitään käänteismatriisia matriisille
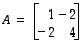 .
.
Muodostetaan kaavio 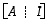 ja muokataan sitä samoilla säännöillä kuin aikaisemminkin. Se saadaan silloin muotoon
ja muokataan sitä samoilla säännöillä kuin aikaisemminkin. Se saadaan silloin muotoon
 .
.
Vastaan tuli epätosi yhtälö 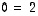 (ja myös
(ja myös 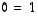 ), joten päätelmänä on, että matriisilla
), joten päätelmänä on, että matriisilla 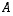 ei ole käänteismatriisia. Se ei siis ole kääntyvä matriisi.
ei ole käänteismatriisia. Se ei siis ole kääntyvä matriisi.

Esimerkki 8.14.
Määrätään käänteismatriisi matriisille
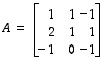 .
.
Muodostetaan ensin kaavio

ja muokataan sitä Gaussin ja Jordanin menetelmän sallimin keinoin ajatellen vain, että oikealla puolella on nyt kolmen eri yhtälöryhmän vakiotermit ja niitä muokataan yhtäaikaisesti. Vähennetään ensimmäinen rivi aluksi kahdella kerrottuna toisesta rivistä ja lisätään se sitten samalla kolmanteen riviin. Silloin saadaan kaavio
 .
.
Nollaamalla toisen rivin avulla toisen sarakkeen alkiot ylä- ja alapuolelta (sekä muuttamalla toisen rivin lukujen merkit) saadaan kaavio
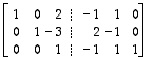 .
.
Kolmannen rivin avulla nollataan lopuksi kolmannen sarakkeen alkioita ja saadaan kaavio
 .
.
Saatiin aikaan kaavio, jossa vasemmalla puolella on yksikkömatriisi. Tämä osoittaa, että lähtömatriisi 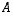 on kääntyvä matriisi. Lisäksi sen käänteismatriisi voidaan nyt lukea kaavion oikealta puolelta. Tuloksena on siten, että
on kääntyvä matriisi. Lisäksi sen käänteismatriisi voidaan nyt lukea kaavion oikealta puolelta. Tuloksena on siten, että
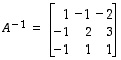 .
.
Tuloksen voi tarkistaa kertomalla matriisit 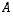 ja
ja 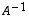 keskenään - kumminpäin tahansa. Tulon on tietenkin oltava yksikkömatriisi kummassakin tapauksessa.
keskenään - kumminpäin tahansa. Tulon on tietenkin oltava yksikkömatriisi kummassakin tapauksessa.

Opiskelutehtävä 31
Etsi käänteismatriisit, jos mahdollista, matriiseille
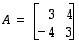 ,
,
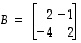 ja
ja 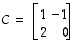 .
.
Vinkki tehtävään 31
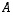 kokoa
kokoa 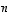 oleva neliömatriisi, jolle käänteismatriisia pyritään etsimään. Merkitään sitä varten muodostetussa yhtälössä
oleva neliömatriisi, jolle käänteismatriisia pyritään etsimään. Merkitään sitä varten muodostetussa yhtälössä 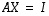 matriisin
matriisin 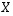 sarakkeita vektoreilla
sarakkeita vektoreilla 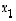 ,
,
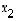 ,
...,
,
..., 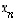 .
Yksikkömatriisin
.
Yksikkömatriisin 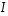 sarakkeet muodostuvat taas kantavektoreista
sarakkeet muodostuvat taas kantavektoreista 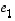 ,
,
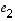 ,
...,
,
..., 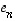 .
Kun matriisilla
.
Kun matriisilla 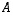 kerrotaan matriisin
kerrotaan matriisin 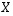 jokin sarake, tulokseksi saadaan tulon
jokin sarake, tulokseksi saadaan tulon 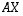 vastaava sarake. Siten matriisiyhtälön
vastaava sarake. Siten matriisiyhtälön 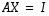 ratkaiseminen on yhtäpitävää vektoriyhtälöiden
ratkaiseminen on yhtäpitävää vektoriyhtälöiden 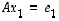 ,
,
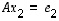 ,
...,
,
..., 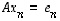 ratkaisemisen kanssa.
ratkaisemisen kanssa. 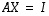 ratkaiseminen voidaan näin ollen tehdä sarakkeittain ja tehtävä voidaan siten periaatteessa paloitella
ratkaiseminen voidaan näin ollen tehdä sarakkeittain ja tehtävä voidaan siten periaatteessa paloitella 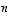 yhtälön ratkaisemiseen. Algoritmisesti nämä yhtälöt voidaan kuitenkin ratkaista yhtäaikaisesti. Jokaisen yhtälön ratkaisemisessahan kerroinmatriisi on aina sama ja siten sen muokkaaminen yksinkertaisempaan muotoon voidaan ajatella tehtävän joka kerta samalla tavalla. Kokonaisuudessaan ideana onkin nyt siis pyrkiä kaaviosta
yhtälön ratkaisemiseen. Algoritmisesti nämä yhtälöt voidaan kuitenkin ratkaista yhtäaikaisesti. Jokaisen yhtälön ratkaisemisessahan kerroinmatriisi on aina sama ja siten sen muokkaaminen yksinkertaisempaan muotoon voidaan ajatella tehtävän joka kerta samalla tavalla. Kokonaisuudessaan ideana onkin nyt siis pyrkiä kaaviosta 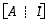 muotoa
muotoa 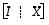 olevaan kaavioon, josta silloin käänteismatriisi
olevaan kaavioon, josta silloin käänteismatriisi 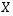 voitaisiin lukea.
voitaisiin lukea. 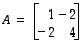 .
.
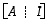 ja muokataan sitä samoilla säännöillä kuin aikaisemminkin. Se saadaan silloin muotoon
ja muokataan sitä samoilla säännöillä kuin aikaisemminkin. Se saadaan silloin muotoon  .
.
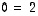 (ja myös
(ja myös 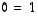 ), joten päätelmänä on, että matriisilla
), joten päätelmänä on, että matriisilla 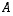 ei ole käänteismatriisia. Se ei siis ole kääntyvä matriisi.
ei ole käänteismatriisia. Se ei siis ole kääntyvä matriisi. 
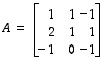 .
.

 .
.
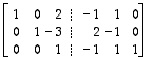 .
.
 .
.
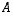 on kääntyvä matriisi. Lisäksi sen käänteismatriisi voidaan nyt lukea kaavion oikealta puolelta. Tuloksena on siten, että
on kääntyvä matriisi. Lisäksi sen käänteismatriisi voidaan nyt lukea kaavion oikealta puolelta. Tuloksena on siten, että 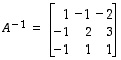 .
.
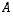 ja
ja 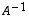 keskenään - kumminpäin tahansa. Tulon on tietenkin oltava yksikkömatriisi kummassakin tapauksessa.
keskenään - kumminpäin tahansa. Tulon on tietenkin oltava yksikkömatriisi kummassakin tapauksessa. 
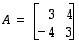 ,
,
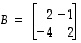 ja
ja 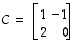 .
.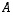 ja
ja 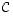 ,
siis että
,
siis että 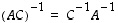 .
.