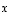 ja
ja 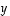 ,
mikä on niiden määräämän suunnikkaan ala?
,
mikä on niiden määräämän suunnikkaan ala?
Aloitetaan taas tasosta ja pyritään ensin vastaamaan seuraavaan kysymykseen. Jos on annettu kaksi vektoria, 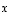 ja
ja 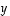 ,
mikä on niiden määräämän suunnikkaan ala?
,
mikä on niiden määräämän suunnikkaan ala?
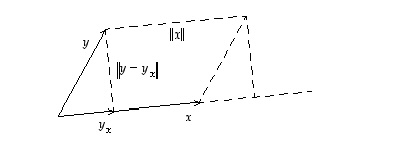
Geometrisesta tarkastelusta nähdään, että kysytty ala saadaan tulona 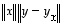 ,
missä
,
missä 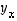 on vektorin
on vektorin 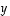 projektio vektorille
projektio vektorille 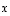 eli
eli
missä vektorin 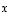 kerrointa on merkitty lyhyesti luvulla
kerrointa on merkitty lyhyesti luvulla 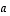 .
Siten
.
Siten 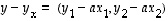 ja
ja
Siten kysytty ala saadaan osoittajan neliöjuuresta eli lausekkeesta 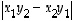 .
.
Itseisarvon sisälle saatua lukua 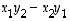 sanotaan vektoreiden
sanotaan vektoreiden 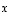 ja
ja  determinantiksi, merkitään
determinantiksi, merkitään 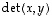 .
Tarkastellun suunnikkaan ala on siis sen määräävien vektorien determinantin itseisarvo. Erikoisesti tästä näkyy, että kyseiset vektorit ovat lineaarisesti riippumattomat täsmälleen silloin, kun niiden määräämän suunnikkaan ala ei ole nolla eli kun niiden determinantti ei ole nolla. Tämä antaa siten uuden kriteerin riippumattomuudelle.
.
Tarkastellun suunnikkaan ala on siis sen määräävien vektorien determinantin itseisarvo. Erikoisesti tästä näkyy, että kyseiset vektorit ovat lineaarisesti riippumattomat täsmälleen silloin, kun niiden määräämän suunnikkaan ala ei ole nolla eli kun niiden determinantti ei ole nolla. Tämä antaa siten uuden kriteerin riippumattomuudelle.
Yleisemmin asetetaankin, että 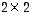 -matriisin
-matriisin
Huomaa, että viimeisimmässä merkinnässä pystyviivat eivät merkitse itseisarvoja. Determinantti voi siis olla yhtä hyvin negatiivinen kuin positiivinenkin luku.
Isompien 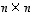 -matriisien determinantti määritellään sitten
kehityssäännöllä seuraavaan tapaan.
-matriisien determinantti määritellään sitten
kehityssäännöllä seuraavaan tapaan.
Jos merkitään, että 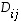 on se
on se 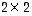 -determinantti, joka saadaan matriisista
-determinantti, joka saadaan matriisista 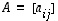 ,
kun siitä poistetaan rivi
,
kun siitä poistetaan rivi 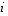 ja sarake
ja sarake 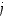 ,
yllä oleva kaava saadaan silloin helpommin muistettavaan muotoon
,
yllä oleva kaava saadaan silloin helpommin muistettavaan muotoon
Huomioi erityisesti kaavassa oleva miinusmerkki.
Laskemalla voidaan osoittaa, että avaruuden 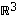 kolmelle vektorille
kolmelle vektorille 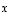 ,
,
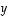 ja
ja 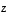 niiden määräämän suuntaissärmiön tilavuus on sen determinantin itseisarvo, joka saadaan sijoittamalla kyseiset vektorit sen sarakkeiksi:
niiden määräämän suuntaissärmiön tilavuus on sen determinantin itseisarvo, joka saadaan sijoittamalla kyseiset vektorit sen sarakkeiksi: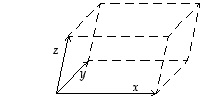
Tapauksessa 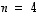 toimitaan yllä olevaa periaatetta jatkaen. Määritellään sen mukaisesti, että
toimitaan yllä olevaa periaatetta jatkaen. Määritellään sen mukaisesti, että 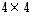 -matriisin
-matriisin 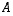 determinantti on luku
determinantti on luku
missä 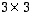 -determinantit
-determinantit 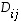 saadaan alkuperäisestä determinantista poistamalla rivi
saadaan alkuperäisestä determinantista poistamalla rivi 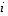 ja sarake
ja sarake 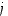 .
.
Yleisesti 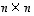 -matriisin
-matriisin 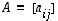 (missä
(missä 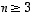 )
determinantti määritellään
kehityssäännöllä (tai
palautussäännöllä)
)
determinantti määritellään
kehityssäännöllä (tai
palautussäännöllä)
missä 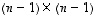 -determinantit
-determinantit 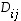 saadaan alkuperäisestä determinantista poistamalla rivi
saadaan alkuperäisestä determinantista poistamalla rivi 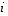 ja sarake
ja sarake 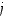 .
Näitä determinantteja sanotaan myös koko determinantin
alideterminanteiksi.
.
Näitä determinantteja sanotaan myös koko determinantin
alideterminanteiksi.
Yllä annettua determinantin laskutapaa sanotaan tarkemmin sen kehittämiseksi ensimmäisen rivin suhteen. Sama tulos saadaan kyllä aikaan, jos se kehitetään vastaavalla tavalla minkä tahansa rivin suhteen - tai jopa myös sarakkeen suhteen. Esimerkiksi determinantti voidaan kehittää rivin 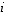 suhteen seuraavasti:
suhteen seuraavasti:
Vastaavasti sarakkeen 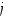 suhteen kehitettynä on
suhteen kehitettynä on
Näiden tulosten todistamiset vaativat kuitenkin laajahkoja tarkasteluja ja ne sivuutetaan sen takia tässä kirjassa. Yllä mainittuja eri rivien ja sarakkeitten mukaan tapahtuvia determinantin kehittämisiä voidaan hyödyntää silloin, jos kehittämiseen voidaan käyttää sellaista riviä tai saraketta, jossa on paljon nollia. Determinantin kehittäminen ensimmäisen rivin suhteen on kuitenkin riittävä keino.
Luvuille 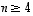 determinantin itseisarvo ilmoittaa sellaisen yleistetyn
determinantin itseisarvo ilmoittaa sellaisen yleistetyn 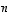 -ulotteisen suuntaissärmiön mitan (yleistetyn tilavuuden), jonka determinantin sarakkeista muodostetut vektorit määräävät. Erityisesti determinantti on sen mukaan nolla täsmälleen silloin, kun sen sarakevektorit ovat lineaarisesti riippuvat. Näiden tulosten täsmälliset matemaattiset todistukset jätetään kuitenkin niiden laajuuden vuoksi tässä kirjassa käsittelemättä.
-ulotteisen suuntaissärmiön mitan (yleistetyn tilavuuden), jonka determinantin sarakkeista muodostetut vektorit määräävät. Erityisesti determinantti on sen mukaan nolla täsmälleen silloin, kun sen sarakevektorit ovat lineaarisesti riippuvat. Näiden tulosten täsmälliset matemaattiset todistukset jätetään kuitenkin niiden laajuuden vuoksi tässä kirjassa käsittelemättä.
Kehityssäännöllä isokokoisen determinantin laskeminen palautetaan siis aina yksi ulottuvuus kerrallaan pienempikokoisten determinanttien laskemiseen, kunnes päästään lopulta kaksiulotteisiin determinantteihin. Pahimmillaan 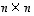 -kokoisen determinantin laskemiseen tarvitaan siten
-kokoisen determinantin laskemiseen tarvitaan siten 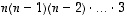 kappaletta
kappaletta 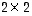 -determinantteja. Menettely on sen takia käytännössä työläs ja tietokoneen suorittamanakin isoille matriiseille aivan liian paljon aikaa vievä. Nopeampi laskutapa saadaan mm. käyttämällä Gaussin ja Jordanin menetelmää hyväksi. Siihen palataan vielä tämän luvun loppupuolella (ks. Determinantin laskeminen Gaussin ja Jordanin menetelmällä).
-determinantteja. Menettely on sen takia käytännössä työläs ja tietokoneen suorittamanakin isoille matriiseille aivan liian paljon aikaa vievä. Nopeampi laskutapa saadaan mm. käyttämällä Gaussin ja Jordanin menetelmää hyväksi. Siihen palataan vielä tämän luvun loppupuolella (ks. Determinantin laskeminen Gaussin ja Jordanin menetelmällä).