Lause 10.5.

Kolmiomatriisin determinantti on sen lävistäjäalkioiden tulo.

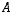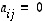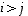Todistus. Olkoon yläkolmiomatriisi, ts. , aina kun . Kun sen determinantti kehitetään ensimmäisen rivin suhteen, voidaan päätellä, että alideterminanteista vain ensimmäinen 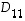on nollasta eroava. Siten 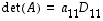. Tämä alideterminantti 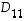on myös yläkolmiotyyppiä. Kun sitä edelleen kehitetään ensimmäisen rivin suhteen, nähdään taas, että 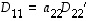, missä determinantti 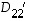saadaan nyt alkuperäisestä matriisista 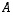poistamalla sen kaksi ensimmäistä riviä ja saraketta. Siten 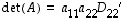. Näin jatkamalla on ilmeistä, että lävistäjäalkiot tulevat determinanttiin kerrotuksi peräjälkeen.

 

Gaussin ja Jordanin menetelmässä sallittuja toimenpiteitä yhtälöryhmän ratkaisemiseksi olivat seuraavat:

(1)   Rivin kertominen nollasta eroavalla luvulla.

(2)   Kahden rivin vaihto.

(3)   Rivin monikerran lisääminen toiseen riviin.

Matriisiteknisesti nämä toimenpiteet saadaan aikaiseksi kertomalla sopivilla matriiseilla yhtälöryhmän kerroinmatriisia .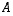

Tapauksessa (1) kerrotaan matriisi 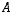vasemmalta sellaisella diagonaalimatriisilla, jonka muut lävistäjäalkiot ovat ykkösiä paitsi kerrottavalla rivillä oleva luku on sama kuin kertojana oleva luku 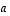. Yllä olevan lauseen 10.5 mukaan tällaisen matriisin determinantti on .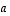

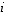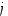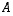Jos tapauksessa (2) halutaan vaihtaa rivit ja , kerrotaan matriisi vasemmalta matriisilla, joka saadaan yksikkömatriisista vaihtamalla paikoiss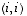a ja 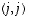olevat ykköset paikoiss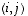a ja 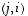olevien nollien kanssa. Tällaisen matriisin determinantti on aina .

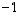Jos tapauksessa (3) halutaan matriisin 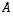rivi 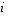lisätä luvulla 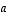kerrottuna riviin 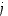, tämä saadaan aikaan kertomalla matriisi 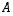vasemmalta matriisilla, jonka kaikki diagonaalialkiot ovat ykkösiä, paikassa 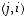on luku 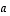ja kaikki muut alkiot ovat nollia. Tällaisen kolmiomatriisin determinantti on aina .

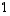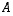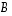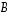Ajatellaan nyt, että matriisi (ilman mitään vakiotermien muodostamaa lisäsaraketta) muunnetaan Gaussin ja Jordanin menetelmän menoalgoritmin mukaisesti yläkolmiomatriisiksi . Silloin matriisin determinantti on edellä olevan lauseen mukaisesti lävistäjäalkioiden tulo. Toisaalta matriisi 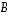voidaan edellä kuvatun mukaisesti ajatella saatavan matriisista 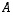kertomalla sitä mainitunlaisilla korjausmatriiseilla ja siten sen determinantti on matriisin 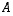determinantti kerrottuna korjausmatriisien determinanteilla. Täten alkuperäisen matriisin 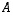determinantti saadaan kolmiomatriisin 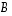determinantista jakamalla korjausmatriisien determinanteilla. Tämä menettely vaatii siis, että algoritmissa tyyppiä (1) ja (2) olevat muunnokset kirjataan ylös, jotta tiedetään miten saadun kolmiomatriisin determinanttia tulee korjata. Tyypin (1) muunnoksissa kerroin 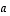tulee ottaa huomioon determinantti jakavana tekijänä ja tyypin (2) muunnokset muuttavat merkkiä. Tyypin (3) muunnokset eivät onneksi muuta determinanttia ja onkin suositeltavaa pyrkiä käyttämään vain niitä.

Esimerkki 10.6.

Lasketaan determinantti

 

Gaussin ja Jordanin menetelmän avulla. Aloitetaan jakamalla ensimmäinen rivi kakkosella:

.

Muutetaan ensimmäisen rivin avulla muut ensimmäisen sarakkeen luvut nolliksi:

.

Vaihdetaan toinen ja kolmas rivi:

.

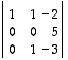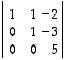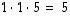On saatu tulokseksi yläkolmiodeterminantti, jonka arvo on . Toisaalta algoritmin aikana on kerran rivi kerrottu luvulla 1/2 ja kerran on vaihdettu kaksi riviä keskenään, joten edellä olevan tarkastelun mukaan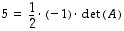

.

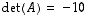Rivin muokkaaminen toisen rivin avulla ei vaikuttanut determinanttiin. Siten .

 

Havainnollistus: Determinantin laskeminen (1)

Havainnollistus: Determinantin laskeminen (2)