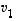 ,
,
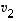 ,
...,
,
..., 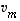 muodostavat avaruuden
muodostavat avaruuden 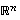 kannan, jos ne ovat lineaarisesti riippumattomat ja virittävät koko avaruuden
kannan, jos ne ovat lineaarisesti riippumattomat ja virittävät koko avaruuden 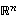 .
Perusesimerkkinä kannasta on luonnollinen kanta
.
Perusesimerkkinä kannasta on luonnollinen kanta 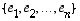 (ks. Yleinen avaruus). Onko muita kantoja?
(ks. Yleinen avaruus). Onko muita kantoja?
Sanotaan, että vektorit 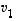 ,
,
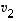 ,
...,
,
..., 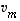 muodostavat avaruuden
muodostavat avaruuden 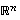 kannan, jos ne ovat lineaarisesti riippumattomat ja virittävät koko avaruuden
kannan, jos ne ovat lineaarisesti riippumattomat ja virittävät koko avaruuden 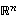 .
Perusesimerkkinä kannasta on luonnollinen kanta
.
Perusesimerkkinä kannasta on luonnollinen kanta 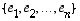 (ks. Yleinen avaruus). Onko muita kantoja?
(ks. Yleinen avaruus). Onko muita kantoja?
Tason vektorit 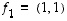 ja
ja 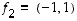 ovat selvästi lineaarisesti riippumattomat (sillä kumpikaan ei ole toisen monikerta) ja toisaalta jokaisella vektorilla
ovat selvästi lineaarisesti riippumattomat (sillä kumpikaan ei ole toisen monikerta) ja toisaalta jokaisella vektorilla 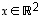 on jokin esitys
on jokin esitys 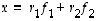 kuten tämän luvun alussa todettiin. Siten ne muodostavat erään tason kannan luonnollisen kannan
kuten tämän luvun alussa todettiin. Siten ne muodostavat erään tason kannan luonnollisen kannan 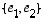 lisäksi. Ainakin tasossa on siten muitakin kantoja. (Tilannetta kuvaa alla oleva kuva.)
lisäksi. Ainakin tasossa on siten muitakin kantoja. (Tilannetta kuvaa alla oleva kuva.)
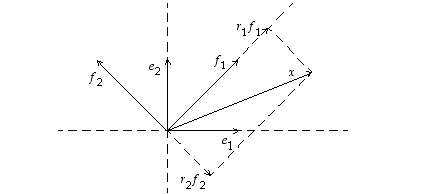
(a) Perustele mahdollisimman lyhyesti, miksi vektorit 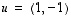 ja
ja 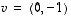 kelpaavat tason kannaksi.
kelpaavat tason kannaksi.
(b) Valitse jokin vektori ja esitä se kannassa 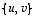 .
Tee se sekä piirtämällä että laskemalla!
.
Tee se sekä piirtämällä että laskemalla!
Edellä todistetulla lauseella 4.8 on monta hyödyllistä seurausta, joista tärkein ilmenee lauseessa 4.13.
Jos vektorit 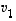 ,
,
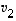 ,
...,
,
..., 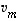 ovat lineaarisesti riippumattomat ja jos vektori
ovat lineaarisesti riippumattomat ja jos vektori 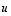 ei ole näiden virittämä, ovat myös vektorit
ei ole näiden virittämä, ovat myös vektorit 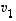 ,
,
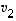 ,
...,
,
..., 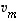 ,
,
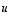 lineaarisesti riippumattomat.
lineaarisesti riippumattomat.
Jos tässä 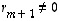 ,
niin voidaan ratkaista
,
niin voidaan ratkaista
Tällöin vektori 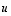 olisi vektorien
olisi vektorien 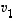 ,
,
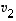 ,
...,
,
..., 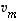 lineaarikombinaatio vastoin oletusta. Siispä
lineaarikombinaatio vastoin oletusta. Siispä 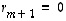 ,
jolloin
,
jolloin 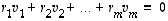 .
Vektorien
.
Vektorien 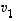 ,
,
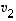 ,
...,
,
..., 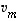 lineaarisen riippumattomuuden perusteella on tällöin myös
lineaarisen riippumattomuuden perusteella on tällöin myös 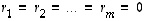 .
Siten kaikki kertoimet ovat nollia. Väite on osoitettu.
.
Siten kaikki kertoimet ovat nollia. Väite on osoitettu.
Jokainen avaruuden 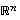 lineaarisesti riippumaton vektorijoukko
lineaarisesti riippumaton vektorijoukko 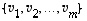 voidaan täydentää sen kannaksi (tarkoittaen, että joko se on jo kanta tai sitten se voidaan muita vektoreita lisäämällä laajentaa kannaksi).
voidaan täydentää sen kannaksi (tarkoittaen, että joko se on jo kanta tai sitten se voidaan muita vektoreita lisäämällä laajentaa kannaksi).
Todistus.
Oletetaan, että annettu vektorijoukko 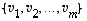 ei vielä viritä koko avaruutta
ei vielä viritä koko avaruutta 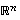 (muutoinhan lauseen väite pitää ilman muuta paikkansa). Valitaan luonnolliset kantavektorit
(muutoinhan lauseen väite pitää ilman muuta paikkansa). Valitaan luonnolliset kantavektorit 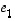 ,
,
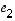 ,
...,
,
..., 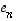 avaruuden
avaruuden 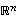 virittäväksi vektorijoukoksi. Lauseen 4.8 mukaan on tällöin
virittäväksi vektorijoukoksi. Lauseen 4.8 mukaan on tällöin 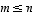 .
.
Nyt jokin vektoreista 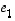 ,
,
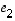 ,
...,
,
..., 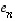 ei virity vektoreilla
ei virity vektoreilla 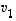 ,
,
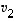 ,
...,
,
..., 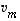 ts. se ei ole näiden lineaarikombinaatio. Lauseen 4.10 mukaan se voidaan tällöin lisätä vektorien
ts. se ei ole näiden lineaarikombinaatio. Lauseen 4.10 mukaan se voidaan tällöin lisätä vektorien 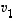 ,
,
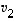 ,
...,
,
..., 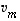 joukkoon näistä lineaarisesti riippumattomana vektorina. Tämän joukon laajentamista luonnollisen kannan vektoreilla jatketaan, kunnes vastaan tulee lineaarisesti riippumaton vektorijoukko, joka virittää koko avaruuden. Koska lauseen 4.8 mukaan lineaarisesti riippumattomassa vektorijoukossa voi olla korkeintaan
joukkoon näistä lineaarisesti riippumattomana vektorina. Tämän joukon laajentamista luonnollisen kannan vektoreilla jatketaan, kunnes vastaan tulee lineaarisesti riippumaton vektorijoukko, joka virittää koko avaruuden. Koska lauseen 4.8 mukaan lineaarisesti riippumattomassa vektorijoukossa voi olla korkeintaan 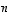 vektoria, tällainen joukko tulee todella jossain vaiheessa vastaan. Se on silloin lauseessa etsitty kanta.
vektoria, tällainen joukko tulee todella jossain vaiheessa vastaan. Se on silloin lauseessa etsitty kanta.
(a) Jokainen avaruuden 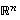 vektorijoukko
vektorijoukko 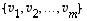 ,
missä
,
missä 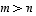 ,
on lineaarisesti riippuva.
,
on lineaarisesti riippuva.
(b) Mikään avaruuden 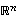 vektorijoukko
vektorijoukko 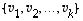 ,
missä
,
missä 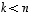 ,
ei voi virittää sitä.
,
ei voi virittää sitä.
Todistus.
Koska luonnolliset kantavektorit 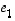 ,
,
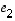 ,
...,
,
..., 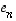 ovat lineaarisesti riippumattomat ja virittävät koko avaruuden, lauseen 4.8 mukaan toisaalta missä tahansa lineaarisesti riippumattomassa joukossa on korkeintaan
ovat lineaarisesti riippumattomat ja virittävät koko avaruuden, lauseen 4.8 mukaan toisaalta missä tahansa lineaarisesti riippumattomassa joukossa on korkeintaan 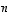 vektoria ja toisaalta missä tahansa virittäjäjoukossa on vähintään
vektoria ja toisaalta missä tahansa virittäjäjoukossa on vähintään 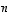 vektoria. Tämä todistaa molemmat väitteet.
vektoria. Tämä todistaa molemmat väitteet.