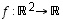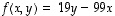Harjoitustehtäviä

1.   Ovatko seuraavat kuvaukset lineaarisia?

(a) , .

(b) , .

(c) , .

Vastaa kysymykseen ensin määritelmän kautta. Miten voisit nähdä lineaarisuuden nopeammin?

2.   Lineaarikuvauksesta 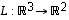tiedetään, että 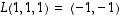, 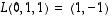ja .

(a) Määrää .

(b) Määrää yleisesti .

(c) Määrää ydin .

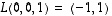(d) Onko 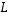injektio? Entä surjektio?

(e) Keksi vähintään kolme eri ratkaisua yhtälölle 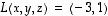. Missä muodossa voit esittää kaikki ratkaisut?

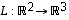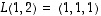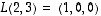3.   Selvitä, onko olemassa sellaista lineaarikuvausta , jolle olisi , ja .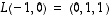

4.   Tason eräs kuvaus kuvaa oikeanpuoleisen kirjaimen F vasemmanpuoleiseksi vinoksi F:ksi. Perustele, miksi se ei voi olla lineaarikuvaus.

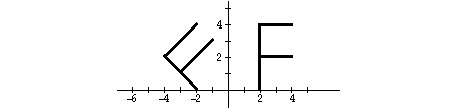
Jos sitten oletetaan, että jokin lineaarikuvaus kuvaa F:n pystyjanan I kuten kuvassa, niin selvitä miten se kuvaa silloin F:n vaakasakarat. (Lue janan koordinaatit kokonaislukuina kuvasta.)

5.   Johda sen lineaarikuvauksen lauseke, joka peilaa 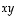-tason pisteet yhtälön 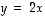eli vektorin 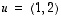määräämän suoran suhteen. (Vihje: Selvitä ensin esimerkiksi projektioiden avulla kantavektoreiden kuvautuminen ja johda niistä sitten lineaarisuussäännöillä yleinen lauseke. Vastaus: . )

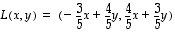6.   Määrää sen lineaarikuvauksen lauseke, joka kiertää tasoa kulman 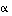verran vastapäivään. (Vihje: Selvitä taas ensin kantavektoreiden kuvautuminen ja johda niistä sitten lineaarisuussäännöillä yleinen lauseke. Vastaukseen tulee sinejä ja kosinejä!)

7.   Osoita, että lineaarikuvauksen 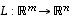kuvajoukko 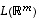on avaruuden 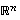aliavaruus (osoittamalla, että se sisältää vektoriensa summat ja monikerrat).