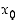Jatkuvuus pisteessä

Raja-arvon avulla voidaan määritellä funktion (kuvaajan) jatkuvuus tarkastelupisteessä. Oletetaan, että funktio on määritelty pisteessä 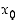ja sen ympäristössä (oikealla tai vasemmalla puolella). Määritellään toispuoleiset jatkuvuudet seuraavasti.

Funktio 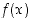on oikealta (op.) jatkuva pisteessä 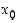, jos

ja vasemmalta (vp.) jatkuva pisteessä 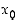, jos

(Ks. kuva 29.)

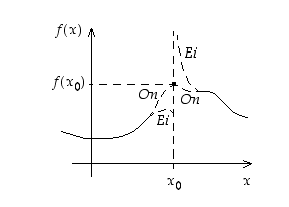
Kuva 29. Onko funktio toispuoleisesti jatkuva?

Edelleen, funktio 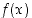on (molemminpuolin) jatkuva pisteessä 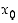, jos se on sekä op. että vp. jatkuva kyseisessä pisteessä, ts. jos

Funktio 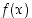on (op./vp.) epäjatkuva määrittelyjoukon pisteessä 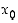, jos se ei ole (op./vp.) jatkuva kyseisessä pisteessä. Tähän voi olla syynä se, että funktiolla ei ole (op./vp.) raja-arvoa ko. pisteessä tai että se on olemassa, mutta eroaa funktion arvosta. Huomaa, että määrittelyn mukaan jatkuvuutta ja epäjatkuvuutta voidaan tarkastella vain funktion määrittelyjoukon pisteessä. Lisäksi funktion täytyy olla määritelty jollain tarkastelupisteen sisältävällä välillä. Eri vaihtoehtoja on havainnollistettu kuvassa 29.

Esimerkki 2.3.1.

Apulauseen 2.2.10 mukaan

kaikille reaaliluvuille 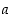ja 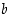. Siten funktio 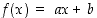on jatkuva jokaisessa pisteessä .

Esimerkki 2.3.2.

Selvitetään, milloin funktio

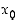on jatkuva pisteessä 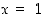. Ensinnäkin edellisen esimerkin mukaan funktio 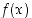on vp. jatkuva pisteessä .

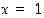On siten selvitettävä vielä, milloin se on op. jatkuva siinä pisteessä. Lauseen 2.2.15 mukaan on

ja toisaalta on 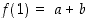. Nämä arvot yhtyvät, kun 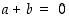eli 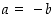. Tämä ehto takaa siten (mp.) jatkuvuuden ko. pisteessä ja on näin ollen myös vastaus esitettyyn kysymykseen.

Esimerkki 2.3.3.

Neliöjuurifunktiolle 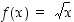on esimerkin 2.2.7 mukaan

joten funktio 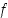on jatkuva pisteissä 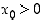. Lisäksi

joten 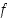on op. jatkuva nollassa. (Vp. jatkuvuutta nollassa ei voi tutkia, koska funktiota ei ole määritelty negatiivisille luvuille.)

Havainnollistus: Neliöönkorotusfunktion jatkuvuus