Rationaalifunktioiden ja trigonometristen funktioiden raja-arvot

Selvitetään yleisesti eräiden säännöllisesti käyttäytyvien lausekkeiden raja-arvojen päätteleminen.

Apulause 2.2.10.

kaikille reaaliluvuille ja .

Todistus. Tapaus 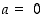on selvä, joten olkoon 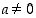. Annetulle on silloin

,

kun .

Lause 2.2.11.

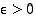(a)  Polynomille on

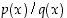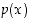(b)  Rationaalifunktiolle , missä ja 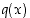ovat polynomeja, on

Todistus. (a) Apulauseessa 2.2.10 on väite todistettu ensimmäisen asteen polynomille. Toisen asteen polynomille 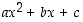on

,

joten edellisen lauseen ja raja-arvojen tulosäännön mukaan

.

Tällekin polynomille lauseen väite siis pätee.

Isompiasteisille polynomeille väite todistetaan induktiivisesti aste kerrallaan edeten. Oletetaan, että väite pätee 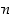−asteisille polynomeille. Olkoon 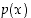sitten 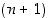−asteinen polynomi, jolloin se voidaan esittää muodos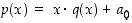sa , missä 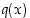on 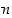−asteinen polynomi ja 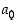on polynomin 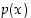vakiotermi. Induktio-oletuksen mukaan

Raja-arvojen rationaalisten laskusääntöjen mukaan on tällöin myös

Siten väite pätee myös polynomille 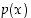. Induktioperiaatteen mukaan väite pätee kaikille polynomeille (sen asteesta riippumatta).

(b) Tulos seuraa raja-arvojen osamääräsäännöstä (lause 2.2.8) edellinen kohta huomioiden.

Esimerkki 2.2.12.

Edellisen lauseen (b)-kohdan mukaan on

Edellä olevaa lausetta ei voi käyttää rationaalifunktioille, joiden nimittäjäpolynomin arvo on nolla tarkastelupisteessä. Mikäli kuitenkin myös osoittajapolynomin arvo on nolla, on rajatuloksena epämääräinen eli määrittelemätön muoto "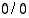", jota ei voi siis määritellä miksikään luvuksi. Tällaisessa tilanteessa molemmilla polynomeilla on kuitenkin sama juuri 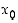, ja siten molemmilla on tekijänä polynomi 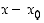. Tämä yhteinen polynomi voidaan supistaa osamäärästä pois ja jatkaa sen jälkeen jäljelle jääneen rationaalilausekkeen tarkastelulla.

Esimerkki 2.2.13.

Määrätään

Sijoittamalla annettuun lausekkeeseen piste 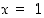saadaan määrittelemätön muoto "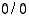". Niinpä osoittaja- ja nimittäjäpolynomeilla on yhteisenä tekijänä polynomi 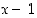. Supistamalla osamäärä tällä polynomilla pystytään raja-arvo sen jälkeen määräämään: Ku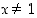n , niin

Sijoittamalla tähän supistettuun lausekkeeseen arvo 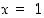, saadaan nyt reaalinen tulos, joka on etsitty raja-arvo. Siis

Mitä voidaan raja-arvosta sanoa, kun 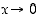? Tällaisiin "epäoleellisiin" raja-arvoihin palataan myöhemmin (ks. Epäoleelliset raja-arvot).

Esimerkki 2.2.14.

Määrätään

(vrt. esimerkki 2.2.1).

Sijoittamalla lausekkeeseen piste 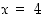saadaan taas määrittelemätön muoto 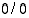. Nimittäjällä on siten tekijänä polynomi 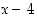. Itse asiassa 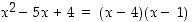. Osoittaja ei kuitenkaan ole polynomi, joten sen "tekijöistä" ei voi tämän perusteella sanoa mitään. Voimme kuitenkin edetä lähes analogisella tavalla kuin edellä. Ajattelemalla polynomia 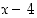neliöiden erotuksena (koska tarkastellaan pisteen 4 ympäristöä, voidaan olettaa, että 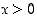) pystytään se kirjoittamaan summan ja erotuksen tulona 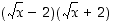. Tätä huomiota käyttäen saadaan raja-arvo pääteltyä: Kun 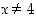, niin

joten

Selvitettävänä ollut raja-arvo on siten 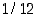.