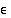 −
−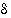 −määrittelyä geometrisesti, kun esimerkkifunktiona on neliöönkorotusfunktio
−määrittelyä geometrisesti, kun esimerkkifunktiona on neliöönkorotusfunktio 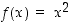 . Kuvassa voi vasemmalla alhaalla olevilla liukukytkimillä säätää tarkastelukohtaa
. Kuvassa voi vasemmalla alhaalla olevilla liukukytkimillä säätää tarkastelukohtaa 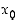 ja muuttujan
ja muuttujan 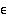 arvoa, jolloin näitä vastaava suurin
arvoa, jolloin näitä vastaava suurin 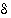 lasketaan valmiiksi.
lasketaan valmiiksi.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tarkoituksena on havainnollistaa jatkuvuuden 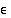 −
−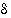 −määrittelyä geometrisesti, kun esimerkkifunktiona on neliöönkorotusfunktio
−määrittelyä geometrisesti, kun esimerkkifunktiona on neliöönkorotusfunktio 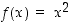 . Kuvassa voi vasemmalla alhaalla olevilla liukukytkimillä säätää tarkastelukohtaa
. Kuvassa voi vasemmalla alhaalla olevilla liukukytkimillä säätää tarkastelukohtaa 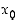 ja muuttujan
ja muuttujan 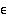 arvoa, jolloin näitä vastaava suurin
arvoa, jolloin näitä vastaava suurin 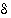 lasketaan valmiiksi.
lasketaan valmiiksi.
Jatkuvuuden määritelmän mukaan:
"Funktio f on jatkuva kohdassa 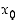 ,
jos kaikilla
,
jos kaikilla 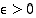 on olemassa
on olemassa 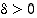 siten, että
siten, että
Geometrisesti tilannetta voidaan havainnollistaa tarkastelupisteen ympärille piirretyllä suorakulmiolla, jonka keskipisteenä tarkastelupiste on. Aluksi valitaan suorakulmion korkeus (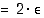 ). Tämän jälkeen tutkitaan, onko suorakulmiolle olemassa sellaista leveyttä (
). Tämän jälkeen tutkitaan, onko suorakulmiolle olemassa sellaista leveyttä (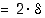 ), että funktion kuvaaja tällä välillä jäisi suorakulmion sisälle. Jos tällaista leveyttä ei löydy, on funktio epäjatkuva kyseisessä kohdassa.
), että funktion kuvaaja tällä välillä jäisi suorakulmion sisälle. Jos tällaista leveyttä ei löydy, on funktio epäjatkuva kyseisessä kohdassa.
Jatkuvuuden osoittamiseksi ei riitä, että tällainen leveys löydetään yhdelle valitulle suorakulmion korkeudelle, vaan on näytettävä, että leveys löytyy kaikille mahdollisille korkeuksille. Tämän vuoksi leveydelle saadaan yleensä lauseke, joka riippuu tarkastelupisteestä ja valitusta korkeudesta.
Tässä tapauksessa leveyden puolikkaalle (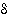 ) on löydetty lauseke tarkastelukohdan ja korkeuden puolikkaan (
) on löydetty lauseke tarkastelukohdan ja korkeuden puolikkaan (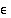 ) avulla, joten funktio on jatkuva. Lauseke on kuvan oikeassa alakulmassa.
) avulla, joten funktio on jatkuva. Lauseke on kuvan oikeassa alakulmassa.
Jos kaipaat haastavaa pohdiskeltavaa, voit miettiä seuraavia kysymyksiä:
b) Miten 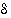 :n lauseke on johdettu?
:n lauseke on johdettu?
Tekstisijainti: Neliöönkorotusfunktion jatkuvuus