VI luku: Alkeisfunktioita
Reaalifunktiot jaetaan algebrallisiin ja transkendenttisiin funktioihin. Algebralliset funktiot ovat sellaisia funktioita 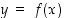 ,
jotka voidaan määritellä implisiittisesti yhtälöllä
,
jotka voidaan määritellä implisiittisesti yhtälöllä 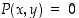 ,
missä
,
missä 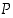 on kahden muuttujan polynomi, jolloin sen lauseke saadaan muuttujista
on kahden muuttujan polynomi, jolloin sen lauseke saadaan muuttujista 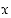 ja
ja 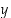 käyttäen vain yhteen-, vähennys- ja kertolaskuja. Algebrallisia funktioita ovat mm. polynomi- ja rationaalifunktiot, joiden lausekkeet muodostuvat yhdestä muuttujasta soveltaen (mahdollisesti toistuvasti) yhteen-, vähennys-, kerto- ja jakolaskuja, sekä irrationaalifunktiot, joiden muodostamiseen käytetään em. rationaalisten laskutoimitusten lisäksi juurenottoja.
käyttäen vain yhteen-, vähennys- ja kertolaskuja. Algebrallisia funktioita ovat mm. polynomi- ja rationaalifunktiot, joiden lausekkeet muodostuvat yhdestä muuttujasta soveltaen (mahdollisesti toistuvasti) yhteen-, vähennys-, kerto- ja jakolaskuja, sekä irrationaalifunktiot, joiden muodostamiseen käytetään em. rationaalisten laskutoimitusten lisäksi juurenottoja.
Muut kuin algebralliset funktiot ovat transkendenttisia funktioita. Tällaisia ovat mm. trigonometriset funktiot sekä tässä luvussa esiteltävät eksponenttifunktiot, logaritmifunktiot, hyperbelifunktiot, areafunktiot ja arkusfunktiot. Algebralliset ja transkendenttiset funktiot sekä näistä saatavat yhdistetyt funktiot muodostavat yleisen ns. alkeisfunktioiden luokan. Muita, esimerkiksi ns. korkeampia transkendenttisia funktioita voidaan muodostaa mm. integraalien ja sarjojen avulla.
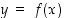 ,
jotka voidaan määritellä implisiittisesti yhtälöllä
,
jotka voidaan määritellä implisiittisesti yhtälöllä 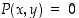 ,
missä
,
missä 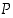 on kahden muuttujan polynomi, jolloin sen lauseke saadaan muuttujista
on kahden muuttujan polynomi, jolloin sen lauseke saadaan muuttujista 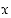 ja
ja 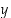 käyttäen vain yhteen-, vähennys- ja kertolaskuja. Algebrallisia funktioita ovat mm. polynomi- ja rationaalifunktiot, joiden lausekkeet muodostuvat yhdestä muuttujasta soveltaen (mahdollisesti toistuvasti) yhteen-, vähennys-, kerto- ja jakolaskuja, sekä irrationaalifunktiot, joiden muodostamiseen käytetään em. rationaalisten laskutoimitusten lisäksi juurenottoja.
käyttäen vain yhteen-, vähennys- ja kertolaskuja. Algebrallisia funktioita ovat mm. polynomi- ja rationaalifunktiot, joiden lausekkeet muodostuvat yhdestä muuttujasta soveltaen (mahdollisesti toistuvasti) yhteen-, vähennys-, kerto- ja jakolaskuja, sekä irrationaalifunktiot, joiden muodostamiseen käytetään em. rationaalisten laskutoimitusten lisäksi juurenottoja.