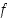 ja
ja 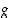 ovat jatkuvia pisteessä
ovat jatkuvia pisteessä 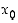 ,
ovat myös funktiot
,
ovat myös funktiot 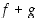 ,
,
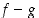 ,
,
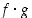 ja
ja 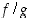 jatkuvia pisteessä
jatkuvia pisteessä 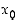 . (Osamäärän kohdalla on oltava lisäksi
. (Osamäärän kohdalla on oltava lisäksi 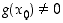 .)
.)
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Seuraava tulos osoittaa, että jossain pisteessä jatkuviksi tunnistetuista funktioista voidaan rationaalisin lausekkein muodostaa uusia jatkuvia funktioita.
Lause 2.3.4. (Rationaalisten lausekkeiden jatkuvuus)
Jos funktiot 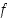 ja
ja 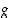 ovat jatkuvia pisteessä
ovat jatkuvia pisteessä 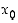 ,
ovat myös funktiot
,
ovat myös funktiot 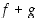 ,
,
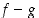 ,
,
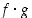 ja
ja 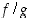 jatkuvia pisteessä
jatkuvia pisteessä 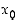 . (Osamäärän kohdalla on oltava lisäksi
. (Osamäärän kohdalla on oltava lisäksi 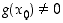 .)
.)
Todistus. Väitteet seuraavat lauseesta 2.2.8.
Toinen tulos seuraa suoraan raja-arvon määrittelystä.
Lause 2.3.5. (Merkin säilyvyys)
Jos funktio 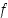 on jatkuva pisteessä
on jatkuva pisteessä 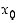 ja
ja 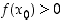 (tai vastaavasti jos
(tai vastaavasti jos 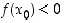 ), on olemassa pisteen
), on olemassa pisteen 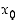 sisältävä avoin väli, jossa funktio
sisältävä avoin väli, jossa funktio 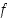 saa vain positiivisia (vast. negatiivisia) arvoja.
saa vain positiivisia (vast. negatiivisia) arvoja.
Todistus. Olkoon 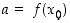 ,
jolloin jatkuvuuden perusteella
,
jolloin jatkuvuuden perusteella
Valitaan 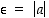 ,
jolloin raja-arvon määrittelyn mukaan on olemassa sellainen
,
jolloin raja-arvon määrittelyn mukaan on olemassa sellainen 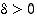 ,
että
,
että
Silloin 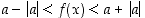 . Tämän mukaan välillä
. Tämän mukaan välillä 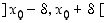 on
on 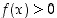 ,
mikäli
,
mikäli 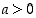 ,
ja
,
ja 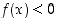 ,
mikäli
,
mikäli 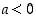 . Väite on todistettu.
. Väite on todistettu.
Lause 2.3.6. (Yhdistetyn kuvauksen jatkuvuus)
Jos funktio 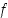 on jatkuva pisteessä
on jatkuva pisteessä 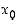 ja funktio
ja funktio 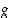 on jatkuva pisteessä
on jatkuva pisteessä 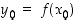 ,
on yhdistetty funktio
,
on yhdistetty funktio 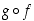 jatkuva pisteessä
jatkuva pisteessä 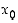 .
.
Todistus. Pitää osoittaa, että jos
Olkoon todistusta varten 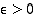 . Funktion
. Funktion 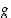 jatkuvuuden perusteella on olemassa sellainen
jatkuvuuden perusteella on olemassa sellainen 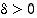 ,
että
,
että
Funktion 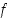 jatkuvuuden perusteella on toisaalta olemassa sellainen
jatkuvuuden perusteella on toisaalta olemassa sellainen 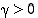 ,
että
,
että
Sijoittamalla edelliseen arvioon 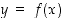 ja
ja 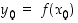 saadaan, että
saadaan, että
Opiskelutehtävä 14. (Funktion jatkuvuus)
Määrää sellainen luku 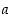 ,
että funktio
,
että funktio