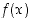 on jossain pisteessä
on jossain pisteessä 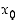 sekä oikean- että vasemmanpuoleinen raja-arvo ja jos ne vielä ovat samat, sanotaan sitä pelkäksi raja-arvoksi tai tarvittaessa tarkemmin molemminpuoleiseksi (mp.) raja-arvoksi,
merkitään
sekä oikean- että vasemmanpuoleinen raja-arvo ja jos ne vielä ovat samat, sanotaan sitä pelkäksi raja-arvoksi tai tarvittaessa tarkemmin molemminpuoleiseksi (mp.) raja-arvoksi,
merkitään
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Jos funktiolla 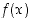 on jossain pisteessä
on jossain pisteessä 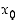 sekä oikean- että vasemmanpuoleinen raja-arvo ja jos ne vielä ovat samat, sanotaan sitä pelkäksi raja-arvoksi tai tarvittaessa tarkemmin molemminpuoleiseksi (mp.) raja-arvoksi,
merkitään
sekä oikean- että vasemmanpuoleinen raja-arvo ja jos ne vielä ovat samat, sanotaan sitä pelkäksi raja-arvoksi tai tarvittaessa tarkemmin molemminpuoleiseksi (mp.) raja-arvoksi,
merkitään
Huomaa, että funktion arvoa tarkastelupisteessä ei nytkään tarvita, joten funktion ei tarvitse olla määritelty siinä pisteessä, jossa raja-arvo halutaan määrätä. Riittää, että se on määritelty tämän pisteen kummallakin puolella.
Edellä olevan esimerkin 2.2.5 mukaan on
Tarkastellaan funktion 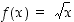 raja-arvoja. Katsotaan ensin pistettä
raja-arvoja. Katsotaan ensin pistettä 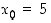 . On ilmeistä, että funktion
. On ilmeistä, että funktion 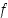 raja-arvo tässä pisteessä on
raja-arvo tässä pisteessä on 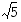 . Osoitetaan tämä arvaus oikeaksi. Koska
. Osoitetaan tämä arvaus oikeaksi. Koska
niin annetulle 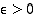 saadaan ehto
saadaan ehto 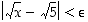 toteutumaan, kun
toteutumaan, kun 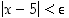 . Silloin nimittäin
. Silloin nimittäin 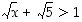 . Siten
. Siten
Samaan tapaan voidaan osoittaa, että yleisesti
(vp. raja-arvoa ei voi tutkia nollassa, koska funktiota 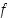 ei ole määritelty negatiivisille luvuille).
ei ole määritelty negatiivisille luvuille).
Edellinen esimerkki osoittaa, että varsin yksinkertaisessakin tilanteessa raja-arvon osoittaminen ennakoidun suuruiseksi voi olla työlästä. Jatkossa pyrimmekin löytämään käyttökelpoisia päättelysääntöjä raja-arvojen määräämiseen.
Opiskelutehtävä 12. (Funktion raja-arvo)
Piirrä seuraavissa kohdissa jonkin sellaisen funktion 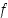 ,
,
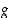 tai
tai 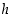 kuvaaja, joka toteuttaa annetut ehdot:
kuvaaja, joka toteuttaa annetut ehdot:
(b) 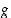 ei ole määritelty pisteessä
ei ole määritelty pisteessä 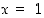 ,
sen oikeanpuoleinen raja-arvo pisteessä
,
sen oikeanpuoleinen raja-arvo pisteessä 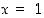 on
on 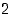 ja vasemmanpuoleinen raja-arvo pisteessä
ja vasemmanpuoleinen raja-arvo pisteessä 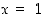 on
on 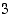 .
.