5.2. Pienin ja suurin arvo suljetulla välillä
Suljetulla välillä jatkuva funktio saa Weierstrassin lauseen mukaan suurimman ja pienimmän arvonsa. Kohdat, joissa funktio ne saa, ovat aina myös paikallisia ääriarvokohtia. Paikallinen ääriarvokohta voi taas olla välin päätepiste, epäjatkuvuuspiste, epäderivoituvuuspiste tai derivaatan nollakohta. Selvittämällä funktion arvot tällaisissa pisteissä löydetään niistä suurin ja pienin arvo.
Esimerkki 5.2.1.
Selvitetään funktion 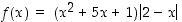 suurin ja pienin arvo suljetulla välillä
suurin ja pienin arvo suljetulla välillä 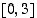 . Funktio
. Funktio 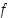 on jatkuva kahden jatkuvan funktion tulona, joten globaalit ääriarvot ovat olemassa. Lisäksi funktio on derivoituva ainakin, kun
on jatkuva kahden jatkuvan funktion tulona, joten globaalit ääriarvot ovat olemassa. Lisäksi funktio on derivoituva ainakin, kun 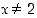 . Ääriarvojen selvittämistä varten ei tarvitse kuitenkaan selvittää derivoituvuutta pisteessä
. Ääriarvojen selvittämistä varten ei tarvitse kuitenkaan selvittää derivoituvuutta pisteessä 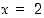 . Riittää, että tämä piste huomioidaan eräänä ehdokkaana ääriarvokohdaksi. Muut ehdokkaat ovat välin päätepisteet ja derivaatan nollakohdat.
. Riittää, että tämä piste huomioidaan eräänä ehdokkaana ääriarvokohdaksi. Muut ehdokkaat ovat välin päätepisteet ja derivaatan nollakohdat.
Derivaatan nollakohtiin ei funktion lausekkeessa oleva itseisarvo vaikuta, joten voimme selvittää funktion
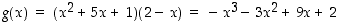
derivaatan nollakohdat. Tämä funktio on sama kuin esimerkin 5.1.8 funktio 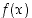 ,
joten kyseiset derivaatan nollakohdat ovat
,
joten kyseiset derivaatan nollakohdat ovat 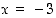 tai
tai 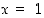 . Näistä edellinen ei kuulu tarkasteltavaan väliin, joten se on jätettävä huomiotta.
. Näistä edellinen ei kuulu tarkasteltavaan väliin, joten se on jätettävä huomiotta.
On saatu neljä ehdokasta ääriarvokohdaksi. Lasketaan funktion arvot niissä kohdissa: 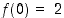 ,
,
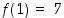 ,
,
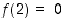 ja
ja 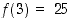 . Näistä suurin 25 on funktion suurin arvo ja pienin 0 on funktion pienin arvo välillä
. Näistä suurin 25 on funktion suurin arvo ja pienin 0 on funktion pienin arvo välillä 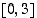 . Katso kuva 46.
. Katso kuva 46.
Kuva 46. Esimerkin 5.2.1 kuva

Havainnollistus: Derivaatta ja ääriarvot 
Opiskeluvideo: K2: Funktion pienimmän ja suurimman arvon selvittäminen 

Ääriarvoja joudutaan usein selvittämään sellaisissa soveltavissa tehtävissä, joissa pyritään minimoimaan tai maksimoimaan esimerkiksi erilaisia kustannuksia.
Esimerkki 5.2.2.
Joen rannalla olevasta sähkövoimalasta halutaan vetää sähkökaapeli joen vastakkaisella puolella olevaan tehtaaseen. Joen leveys on yksi kilometri ja tehdas sijaitsee joen alajuoksulla kahden kilometrin päässä. Kaapelointikustannukset veteen laskettuna ovat kaksinkertaiset maahan kaivamiseen verrattuna. Miten kauas alajuoksulle päin kaapeli kannattaa vetää joen yli, jotta kokonaiskustannukset olisivat pienimmät mahdolliset?
Merkitään, että maahan kaivamisen kustannus on yksi yksikkö kilometriä kohden ja joen yli kaapelointi vedetään kuvan 47 mukaisesti sähkövoimalan S vastarannalta voimalan kohtisuorasta paikasta 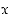 kilometriä tehtaaseen T päin.
kilometriä tehtaaseen T päin.
Kuva 47. Esimerkin 5.2.2 kuva
Silloin kaapeloinnin kustannusfunktio on seuraava:
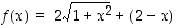 .
.
Tämä funktio on tehtävän luonteesta johtuen järkevää määritellä nyt vain välillä 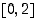 . Määrätään sen pienin arvo. Funktio
. Määrätään sen pienin arvo. Funktio 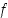 on jatkuva ja derivoituva, joten kyseinen arvo on olemassa. Lasketaan ensin derivaatta
on jatkuva ja derivoituva, joten kyseinen arvo on olemassa. Lasketaan ensin derivaatta
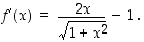
Sen nollakohdaksi saadaan ehdosta 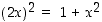 piste
piste 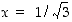 (vastaava negatiivinen juuren arvo ei käy). Pienimmän arvon selvittämiseksi lasketaan funktion arvot päätepisteissä ja derivaatan nollakohdassa:
(vastaava negatiivinen juuren arvo ei käy). Pienimmän arvon selvittämiseksi lasketaan funktion arvot päätepisteissä ja derivaatan nollakohdassa:
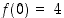 ,
,
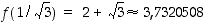 ja
ja 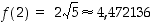 .
.
Näistä keskimmäinen on pienin arvo, joka saatiin arvolla 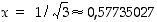 . Kaapeli kannattaa siis vetää vinoon noin 580 metriä tehtaalle päin.
. Kaapeli kannattaa siis vetää vinoon noin 580 metriä tehtaalle päin.

Esimerkki 5.2.3.
Mikä niistä suljetuista lieriöistä, joiden kokonaispinta-ala on vakio, on tilavin?
Kun lieriön pohjan säde on 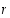 ja korkeus on
ja korkeus on 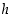 ,
ovat lieriön pinta-ala (vaipan ja pohjien yhteispinta-ala) ja tilavuus
,
ovat lieriön pinta-ala (vaipan ja pohjien yhteispinta-ala) ja tilavuus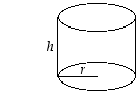
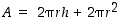 ja
ja 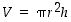
(missä 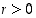 ja
ja 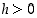 ).
).
Koska ala 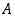 on vakio, määräytyy tällöin edellisestä yhtälöstä korkeus
on vakio, määräytyy tällöin edellisestä yhtälöstä korkeus 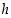 pohjan säteen
pohjan säteen 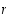 funktiona:
funktiona: 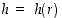 . Implisiittisellä derivoinnilla saadaan alan lausekkeesta yhtälö
. Implisiittisellä derivoinnilla saadaan alan lausekkeesta yhtälö
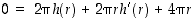 ,
,
mistä saadaan edelleen derivaatalle ratkaisu
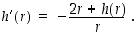
Tilavuusfunktion derivaatta on näin ollen
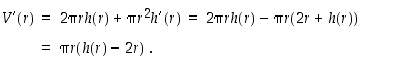
Tämä lauseke on nolla, kun 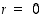 tai
tai 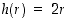 . Näistä edellinen arvo antaisi nollatilavuuden, joten se hylätään. Jälkimmäinen arvo antaa tehtävän luonteen mukaan selvästi maksimitilavuuden.
. Näistä edellinen arvo antaisi nollatilavuuden, joten se hylätään. Jälkimmäinen arvo antaa tehtävän luonteen mukaan selvästi maksimitilavuuden.
Vastaus: Sellainen lieriö, jonka korkeus on kaksi kertaa pohjan säde.

Opiskelutehtävä 29. (Suurimman arvon määrääminen)
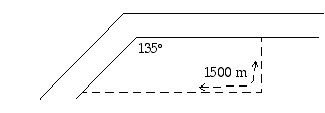
Joki tekee maatilan nurkassa 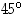 kulman. Tilallinen haluaa rajata kahdella suoralla aidalla laidunmaata joen rannasta niin, että toinen aita on joen suuntainen ja toinen tätä aitaa kohtisuorassa. Joen rantaan ei tarvita aitaa. Hänellä on käytössään yhteensä 1500 metriä aitaa. Kuinka hänen on aita jaettava, jotta hän saisi pinta-alaltaan mahdollisimman suuren laidunmaan.
kulman. Tilallinen haluaa rajata kahdella suoralla aidalla laidunmaata joen rannasta niin, että toinen aita on joen suuntainen ja toinen tätä aitaa kohtisuorassa. Joen rantaan ei tarvita aitaa. Hänellä on käytössään yhteensä 1500 metriä aitaa. Kuinka hänen on aita jaettava, jotta hän saisi pinta-alaltaan mahdollisimman suuren laidunmaan.
Vinkki tehtävään 29
Havainnollistus: Kolmion suurin ala 
Havainnollistus: Laatikon suurin tilavuus 
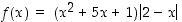 suurin ja pienin arvo suljetulla välillä
suurin ja pienin arvo suljetulla välillä 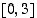 . Funktio
. Funktio 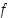 on jatkuva kahden jatkuvan funktion tulona, joten globaalit ääriarvot ovat olemassa. Lisäksi funktio on derivoituva ainakin, kun
on jatkuva kahden jatkuvan funktion tulona, joten globaalit ääriarvot ovat olemassa. Lisäksi funktio on derivoituva ainakin, kun 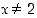 . Ääriarvojen selvittämistä varten ei tarvitse kuitenkaan selvittää derivoituvuutta pisteessä
. Ääriarvojen selvittämistä varten ei tarvitse kuitenkaan selvittää derivoituvuutta pisteessä 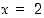 . Riittää, että tämä piste huomioidaan eräänä ehdokkaana ääriarvokohdaksi. Muut ehdokkaat ovat välin päätepisteet ja derivaatan nollakohdat.
. Riittää, että tämä piste huomioidaan eräänä ehdokkaana ääriarvokohdaksi. Muut ehdokkaat ovat välin päätepisteet ja derivaatan nollakohdat. 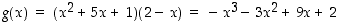
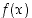 ,
joten kyseiset derivaatan nollakohdat ovat
,
joten kyseiset derivaatan nollakohdat ovat 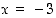 tai
tai 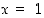 . Näistä edellinen ei kuulu tarkasteltavaan väliin, joten se on jätettävä huomiotta.
. Näistä edellinen ei kuulu tarkasteltavaan väliin, joten se on jätettävä huomiotta. 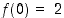 ,
,
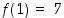 ,
,
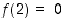 ja
ja 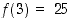 . Näistä suurin 25 on funktion suurin arvo ja pienin 0 on funktion pienin arvo välillä
. Näistä suurin 25 on funktion suurin arvo ja pienin 0 on funktion pienin arvo välillä 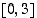 . Katso kuva
. Katso kuva 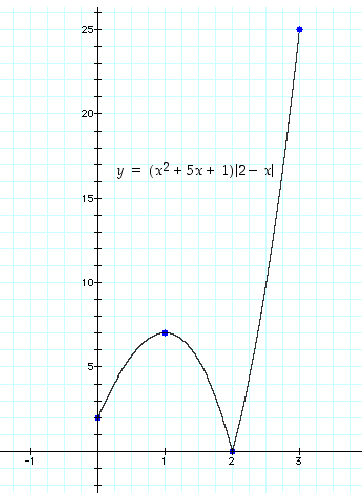



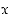 kilometriä tehtaaseen T päin.
kilometriä tehtaaseen T päin. 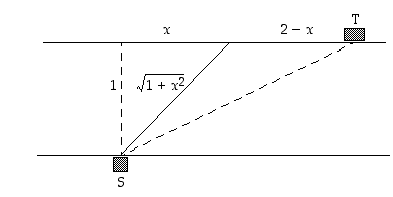
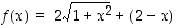 .
. 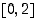 . Määrätään sen pienin arvo. Funktio
. Määrätään sen pienin arvo. Funktio 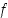 on jatkuva ja derivoituva, joten kyseinen arvo on olemassa. Lasketaan ensin derivaatta
on jatkuva ja derivoituva, joten kyseinen arvo on olemassa. Lasketaan ensin derivaatta 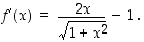
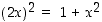 piste
piste 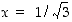 (vastaava negatiivinen juuren arvo ei käy). Pienimmän arvon selvittämiseksi lasketaan funktion arvot päätepisteissä ja derivaatan nollakohdassa:
(vastaava negatiivinen juuren arvo ei käy). Pienimmän arvon selvittämiseksi lasketaan funktion arvot päätepisteissä ja derivaatan nollakohdassa: 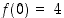 ,
,
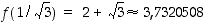 ja
ja 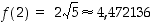 .
. 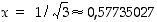 . Kaapeli kannattaa siis vetää vinoon noin 580 metriä tehtaalle päin.
. Kaapeli kannattaa siis vetää vinoon noin 580 metriä tehtaalle päin. 
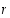 ja korkeus on
ja korkeus on 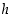 ,
ovat lieriön pinta-ala (vaipan ja pohjien yhteispinta-ala) ja tilavuus
,
ovat lieriön pinta-ala (vaipan ja pohjien yhteispinta-ala) ja tilavuus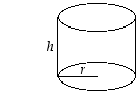
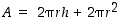 ja
ja 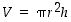
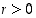 ja
ja 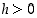 ).
). 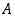 on vakio, määräytyy tällöin edellisestä yhtälöstä korkeus
on vakio, määräytyy tällöin edellisestä yhtälöstä korkeus 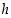 pohjan säteen
pohjan säteen 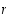 funktiona:
funktiona: 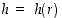 . Implisiittisellä derivoinnilla saadaan alan lausekkeesta yhtälö
. Implisiittisellä derivoinnilla saadaan alan lausekkeesta yhtälö 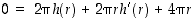 ,
,
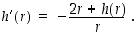
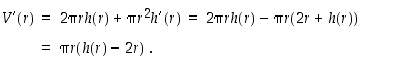
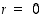 tai
tai 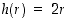 . Näistä edellinen arvo antaisi nollatilavuuden, joten se hylätään. Jälkimmäinen arvo antaa tehtävän luonteen mukaan selvästi maksimitilavuuden.
. Näistä edellinen arvo antaisi nollatilavuuden, joten se hylätään. Jälkimmäinen arvo antaa tehtävän luonteen mukaan selvästi maksimitilavuuden. 
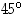 kulman. Tilallinen haluaa rajata kahdella suoralla aidalla laidunmaata joen rannasta niin, että toinen aita on joen suuntainen ja toinen tätä aitaa kohtisuorassa. Joen rantaan ei tarvita aitaa. Hänellä on käytössään yhteensä 1500 metriä aitaa. Kuinka hänen on aita jaettava, jotta hän saisi pinta-alaltaan mahdollisimman suuren laidunmaan.
kulman. Tilallinen haluaa rajata kahdella suoralla aidalla laidunmaata joen rannasta niin, että toinen aita on joen suuntainen ja toinen tätä aitaa kohtisuorassa. Joen rantaan ei tarvita aitaa. Hänellä on käytössään yhteensä 1500 metriä aitaa. Kuinka hänen on aita jaettava, jotta hän saisi pinta-alaltaan mahdollisimman suuren laidunmaan.