Toinen ääriarvotesti
Myös toisen derivaatan avulla voidaan paikallisen ääriarvon tyyppi (maksimi tai minimi) määrätä.
Lause 5.1.7. (2. ääriarvotesti)
Oletetaan, että funktio 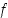 on derivoituva pisteen
on derivoituva pisteen 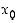 sisältävällä avoimella välillä,
sisältävällä avoimella välillä, 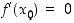 ja
ja 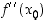 on olemassa. Jos tällöin
on olemassa. Jos tällöin 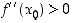 ,
on piste
,
on piste 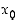 funktion
funktion 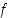 paikallinen minimikohta, jos taas
paikallinen minimikohta, jos taas 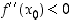 ,
on
,
on 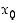 funktion
funktion 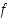 paikallinen maksimikohta. (Tapauksessa
paikallinen maksimikohta. (Tapauksessa 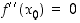 ei voi sanoa tämän perusteella mitään.)
ei voi sanoa tämän perusteella mitään.)
Todistus. Jos 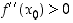 ,
on derivaatta
,
on derivaatta 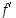 kasvava pisteen
kasvava pisteen 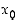 ympäristössä ja siten sen merkki muuttuu pisteessä
ympäristössä ja siten sen merkki muuttuu pisteessä 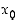 negatiivisesta positiiviseksi. Edellisen lauseen mukaan piste
negatiivisesta positiiviseksi. Edellisen lauseen mukaan piste 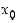 funktion
funktion 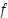 paikallinen minimikohta.
paikallinen minimikohta.
Vastaavasti tilanteessa 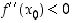 derivaatta
derivaatta 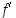 on vähenevä, joten sen merkki muuttuu pisteessä
on vähenevä, joten sen merkki muuttuu pisteessä 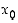 positiivisesta negatiiviseksi ja näin ollen piste
positiivisesta negatiiviseksi ja näin ollen piste 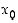 on funktion
on funktion 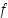 paikallinen maksimikohta.
paikallinen maksimikohta.

Esimerkki 5.1.8.
Tutkitaan funktion 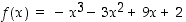 ääriarvoja. Funktio
ääriarvoja. Funktio 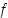 on polynomina kaikkialla jatkuva ja derivoituva. Selvitetään funktion
on polynomina kaikkialla jatkuva ja derivoituva. Selvitetään funktion 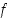 derivaatan nollakohdat. Derivaatta on
derivaatan nollakohdat. Derivaatta on 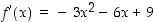 ,
joten
,
joten 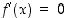 ,
kun
,
kun 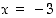 tai
tai 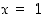 . On saatu siten kaksi ehdokasta ääriarvokohdiksi.
. On saatu siten kaksi ehdokasta ääriarvokohdiksi.
Selvitetään sitten, ovatko saadut ehdokkaat todellisia ääriarvokohtia. Tehdään se ensin 1. ääriarvotestin mukaisesti. Jatkuvuuden ja derivaatan merkin säilyvyyden perusteella funktio on aidosti monotoninen väleillä 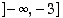 ,
,
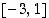 ja
ja 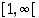 . Monotonisuuden laadun selvittämiseksi riittää nyt kullakin välillä verrata funktion arvoja välipisteissä ja päätepisteissä. Esimerkiksi
. Monotonisuuden laadun selvittämiseksi riittää nyt kullakin välillä verrata funktion arvoja välipisteissä ja päätepisteissä. Esimerkiksi 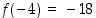 ja
ja 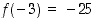 ,
joten
,
joten 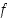 on aidosti vähenevä välillä
on aidosti vähenevä välillä 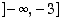 . Vastaavasti arvojen
. Vastaavasti arvojen 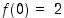 ,
,
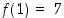 ja
ja 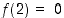 perusteella
perusteella 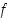 on aidosti kasvava välillä
on aidosti kasvava välillä 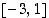 ja aidosti vähenevä välillä
ja aidosti vähenevä välillä 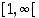 . Samat monotonisuustulokset voi päätellä myös siitä, että derivaatan kuvaaja on alaspäin aukeava paraabeli, mistä sen merkit voi helposti päätellä. Kohdat
. Samat monotonisuustulokset voi päätellä myös siitä, että derivaatan kuvaaja on alaspäin aukeava paraabeli, mistä sen merkit voi helposti päätellä. Kohdat 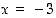 ja
ja 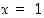 ovat siis paikallisia ääriarvokohtia, edellinen paikallinen minimikohta ja jälkimmäinen paikallinen maksimikohta.
ovat siis paikallisia ääriarvokohtia, edellinen paikallinen minimikohta ja jälkimmäinen paikallinen maksimikohta.
Ääriarvojen tyypin määrittely voidaan tehdä myös 2. ääriarvotestin mukaisesti. Funktion 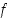 toinen derivaatta
toinen derivaatta 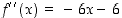 on kaikkialla olemassa ja saa pisteissä
on kaikkialla olemassa ja saa pisteissä 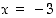 ja
ja 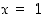 arvot
arvot 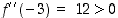 ja
ja 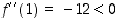 ,
joten nyt myös tämän ääriarvotestin perusteella pisteet
,
joten nyt myös tämän ääriarvotestin perusteella pisteet 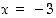 ja
ja 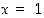 ovat paikallisia ääriarvokohtia, edellinen paikallinen minimikohta ja jälkimmäinen paikallinen maksimikohta.
ovat paikallisia ääriarvokohtia, edellinen paikallinen minimikohta ja jälkimmäinen paikallinen maksimikohta.
Kumpikaan paikallinen ääriarvokohta ei ole globaali ääriarvokohta. Katso kuva 45.
Kuva 45. Esimerkin 5.1.8 kuva

Opiskeluvideo: K1: Funktion ääriarvot 

Opiskelutehtävä 28. (Funktion ääriarvot ja monotonisuus)
Mitä voit sanoa funktiosta 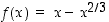 välillä
välillä 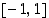 ? Määrää ääriarvot ja monotonisuusalueet. Millainen se on tämän välin ulkopuolella?
? Määrää ääriarvot ja monotonisuusalueet. Millainen se on tämän välin ulkopuolella?
Vinkki tehtävään 28
Havainnollistus: Testaa tietosi derivaatasta 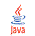
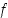 on derivoituva pisteen
on derivoituva pisteen 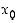 sisältävällä avoimella välillä,
sisältävällä avoimella välillä, 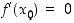 ja
ja 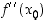 on olemassa. Jos tällöin
on olemassa. Jos tällöin 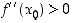 ,
on piste
,
on piste 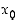 funktion
funktion 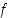 paikallinen minimikohta, jos taas
paikallinen minimikohta, jos taas 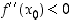 ,
on
,
on 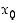 funktion
funktion 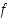 paikallinen maksimikohta. (Tapauksessa
paikallinen maksimikohta. (Tapauksessa 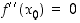 ei voi sanoa tämän perusteella mitään.)
ei voi sanoa tämän perusteella mitään.) 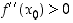 ,
on derivaatta
,
on derivaatta 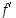 kasvava pisteen
kasvava pisteen 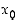 ympäristössä ja siten sen merkki muuttuu pisteessä
ympäristössä ja siten sen merkki muuttuu pisteessä 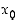 negatiivisesta positiiviseksi. Edellisen lauseen mukaan piste
negatiivisesta positiiviseksi. Edellisen lauseen mukaan piste 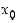 funktion
funktion 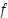 paikallinen minimikohta.
paikallinen minimikohta. 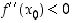 derivaatta
derivaatta 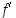 on vähenevä, joten sen merkki muuttuu pisteessä
on vähenevä, joten sen merkki muuttuu pisteessä 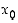 positiivisesta negatiiviseksi ja näin ollen piste
positiivisesta negatiiviseksi ja näin ollen piste 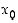 on funktion
on funktion 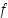 paikallinen maksimikohta.
paikallinen maksimikohta. 
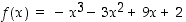 ääriarvoja. Funktio
ääriarvoja. Funktio 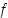 on polynomina kaikkialla jatkuva ja derivoituva. Selvitetään funktion
on polynomina kaikkialla jatkuva ja derivoituva. Selvitetään funktion 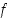 derivaatan nollakohdat. Derivaatta on
derivaatan nollakohdat. Derivaatta on 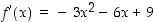 ,
joten
,
joten 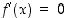 ,
kun
,
kun 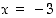 tai
tai 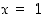 . On saatu siten kaksi ehdokasta ääriarvokohdiksi.
. On saatu siten kaksi ehdokasta ääriarvokohdiksi. 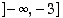 ,
,
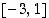 ja
ja 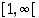 . Monotonisuuden laadun selvittämiseksi riittää nyt kullakin välillä verrata funktion arvoja välipisteissä ja päätepisteissä. Esimerkiksi
. Monotonisuuden laadun selvittämiseksi riittää nyt kullakin välillä verrata funktion arvoja välipisteissä ja päätepisteissä. Esimerkiksi 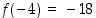 ja
ja 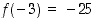 ,
joten
,
joten 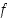 on aidosti vähenevä välillä
on aidosti vähenevä välillä 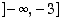 . Vastaavasti arvojen
. Vastaavasti arvojen 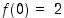 ,
,
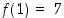 ja
ja 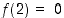 perusteella
perusteella 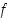 on aidosti kasvava välillä
on aidosti kasvava välillä 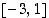 ja aidosti vähenevä välillä
ja aidosti vähenevä välillä 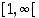 . Samat monotonisuustulokset voi päätellä myös siitä, että derivaatan kuvaaja on alaspäin aukeava paraabeli, mistä sen merkit voi helposti päätellä. Kohdat
. Samat monotonisuustulokset voi päätellä myös siitä, että derivaatan kuvaaja on alaspäin aukeava paraabeli, mistä sen merkit voi helposti päätellä. Kohdat 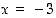 ja
ja 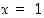 ovat siis paikallisia ääriarvokohtia, edellinen paikallinen minimikohta ja jälkimmäinen paikallinen maksimikohta.
ovat siis paikallisia ääriarvokohtia, edellinen paikallinen minimikohta ja jälkimmäinen paikallinen maksimikohta. 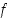 toinen derivaatta
toinen derivaatta 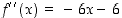 on kaikkialla olemassa ja saa pisteissä
on kaikkialla olemassa ja saa pisteissä 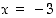 ja
ja 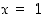 arvot
arvot 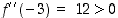 ja
ja 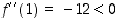 ,
joten nyt myös tämän ääriarvotestin perusteella pisteet
,
joten nyt myös tämän ääriarvotestin perusteella pisteet 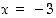 ja
ja 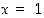 ovat paikallisia ääriarvokohtia, edellinen paikallinen minimikohta ja jälkimmäinen paikallinen maksimikohta.
ovat paikallisia ääriarvokohtia, edellinen paikallinen minimikohta ja jälkimmäinen paikallinen maksimikohta. 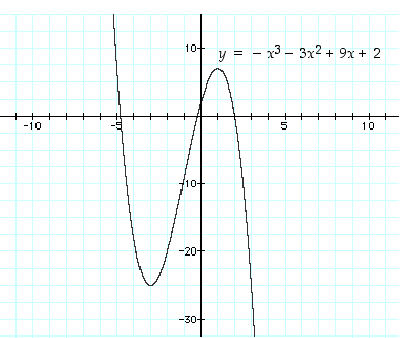



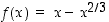 välillä
välillä 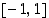 ? Määrää ääriarvot ja monotonisuusalueet. Millainen se on tämän välin ulkopuolella?
? Määrää ääriarvot ja monotonisuusalueet. Millainen se on tämän välin ulkopuolella?