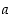,
taitellaan (kanneton) laatikko niin, että pahviarkin nurkista leikataan samankokoiset ja neliön muotoiset palat pois. Kuinka paljon on nurkista leikattava, jotta saadun laatikon tilavuus olisi mahdollisimman suuri?
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Hahmotellaan seuraavan tehtävän ratkaisemista: Neliön muotoisesta pahviarkista, jonka sivun pituus on ,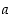
taitellaan (kanneton) laatikko niin, että pahviarkin nurkista leikataan samankokoiset ja neliön muotoiset palat pois. Kuinka paljon on nurkista leikattava, jotta saadun laatikon tilavuus olisi mahdollisimman suuri?
Kuvassa on graafinen hahmotelma tehtävästä. Leikattavan palan kokoa voi muuttaa raahaamalla kuvassa punaista pistettä. Kuvan alla on ideoita, kuinka tehtävän voi ratkaista vaiheittain.
Kuvaan on merkitty muuttujalla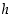 
leikatun neliön sivun pituutta ja muuttujalla 
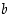sitä osuutta, joka jää leikkauksen jälkeen sivusta jäljelle.
1. Kuvan punaista pistettä siirtämällä voit muuttaa leikattavien palojen suuruutta. Seuraamalla tilavuuden numeerista arvoa ja tilavuusfunktion kuvaajaa arvioi, milloin tilavuus olisi suurimmillaan.
Seuraavassa on ohjeita tehtävän tarkkaan ratkaisemiseen.
2. Mikä on laatikon tilavuus muuttujien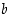 
ja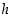 
avulla ilmaistuna?
3. Miten pahviarkin leveys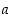 
voidaan ilmaista muuttujien 
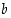ja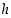 
avulla?
4. Ratkaise saadusta lausekkeesta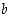 
.
5. Kun sijoitat muuttujan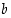 
muuttujien 
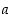ja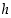 
avulla ilmaistuna tilavuuden lausekkeeseen 
,
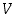saat pahvilaatikon tilavuudelle lausekkeen, joka riippuu vain yhdestä muuttujasta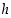 
.
6. Saatiin siis funktio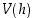 
. Mikä on sen määrittelyväli, kun muistetaan, että 
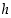on pituutta ilmaiseva muuttuja? (Kuvassa on näkyvissä funktion 
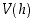kuvaaja.)
7. Mikä on suurin tilavuus, joka voidaan saavuttaa? Tämän ratkaisemiseksi derivoi tilavuusfunktio ja selvitä derivaatan nollakohta!
Tekstisijainti: Laatikon suurin tilavuus