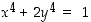ratkaisukäyrän 
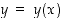pisteiden suurin ja pienin etäisyys origosta.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
157. Määrää yhtälön 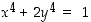ratkaisukäyrän 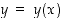pisteiden suurin ja pienin etäisyys origosta.
158. Neliön muotoisesta pahviarkista, jonka sivun pituus on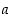 
,
taitellaan (kanneton) laatikko niin, että pahviarkin nurkista leikataan neliön muotoiset palat pois. Kuinka paljon on nurkista leikattava, jotta saadun laatikon tilavuus olisi mahdollisimman suuri?
160. Määrää funktion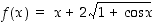 
ääriarvot sekä suurin ja pienin arvo välillä 
.
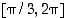161. Tasakylkisen kolmion huippu on tason pisteessä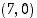 
ja kannan päätepisteet origokeskisen 2−säteisen ympyrän kehällä. Määritä tällaisten kolmioiden suurin mahdollinen ala.
162. Tarkastellaan paraabelin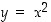 
kuvaajan pisteitä 
,
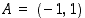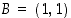ja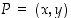 
. Milloin pisteen 
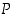etäisyyksien pisteistä 
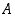ja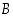 
neliösumma 
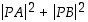on pienin ja milloin suurin mahdollinen?
163. Tarkastellaan tasossa suorakulmioita, jotka ovat ellipsin
sisällä. Mikä on tällaisten suorakulmioiden suurin mahdollinen ala?
ja 
). 