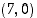Kolmion suurin ala

Havainnollistetaan seuraavaa tehtävää: Tasakylkisen kolmion huippu on tason pisteessä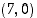

ja kannan päätepisteet origokeskisen 2−säteisen ympyrän kehällä. Määritä tällaisten kolmioiden suurin mahdollinen ala.

Kuvan pistettä C voi liikuttaa ympyrän kehällä. Kuvan yläosassa näkyy kolmioon ABC liittyviä arvoja. Tehtävän ratkaiseminen on jaettu pienempiin osatehtäviin, jotka ovat kuvan jälkeen.

Tehtäviä

1. Mikä näyttäisi olevan kolmion suurin mahdollinen ala?

2. Missä kohti piste C tällöin sijaitsee tasossa ja mitkä ovat kolmion sivujen pituudet?

3. Mikä on tehtävässä määritellyn ympyrän yhtälö?

4. Määritellään muuttuja 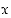siten, että piste F sijaitsee pisteessä 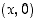. Mikä on tällöin kolmion korkeus AF?

5. Ympyrän kaaren pisteellä C on sama 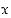−koordinaatti, kuin pisteellä F. Mikä on sen 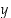−koordinaatti muuttujan 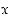avulla ilmaistuna? Kuinka saat tästä tiedosta selville kolmion kannan CB pituuden ilmaistuna 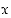:n avulla?

6. Kahdessa edellisessä kohdassa saatiin kolmion korkeus ja kanta ilmaistua 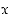:n avulla. Siispä kolmion alakin voidaan nyt ilmaista muuttujan 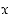avulla. Millainen lauseke kolmion alalle 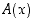saadaan?

7. Mikä on suurin arvo, minkä funktio 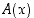voi saada? Toisin sanoen, mikä on kolmion ABC suurin mahdollinen ala? Ratkaisemista varten joudut derivoimaan alan lausekkeen ja selvittämään derivaatan nollakohdat!

Tekstisijainti: Kolmion suurin ala