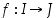 avoimella välillä
avoimella välillä 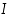 määritelty bijektio, joka on derivoituva pisteessä
määritelty bijektio, joka on derivoituva pisteessä 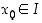 . Oletetaan lisäksi, että
. Oletetaan lisäksi, että 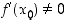 ja että käänteisfunktio
ja että käänteisfunktio 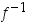 on jatkuva pisteessä
on jatkuva pisteessä 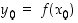 . Tällöin käänteisfunktio
. Tällöin käänteisfunktio 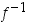 on derivoituva pisteessä
on derivoituva pisteessä 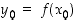 ja
ja
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tarkastellaan derivoituva funktiota, jolla on käänteisfunktio. Jos käänteisfunktion lauseke pystytään ratkaisemaan, voidaan sen derivaatta määrätä derivoimissäännöin. Käyttämällä apuna yhdistetyn funktion derivoimista voidaan käänteisfunktion derivaatta kuitenkin määrätä ilman funktion lausekkeen määräämistä.
Olkoon funktio 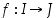 avoimella välillä
avoimella välillä 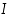 määritelty bijektio, joka on derivoituva pisteessä
määritelty bijektio, joka on derivoituva pisteessä 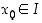 . Oletetaan lisäksi, että
. Oletetaan lisäksi, että 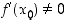 ja että käänteisfunktio
ja että käänteisfunktio 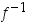 on jatkuva pisteessä
on jatkuva pisteessä 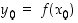 . Tällöin käänteisfunktio
. Tällöin käänteisfunktio 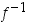 on derivoituva pisteessä
on derivoituva pisteessä 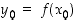 ja
ja
Todistus. Merkitään 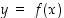 ,
jolloin
,
jolloin 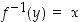 . Käänteisfunktion
. Käänteisfunktion 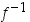 erotusosamäärä pisteessä
erotusosamäärä pisteessä 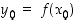 on nyt
on nyt
Käänteisfunktion oletettiin olevan jatkuvan pisteessä 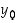 ,
joten ehdosta
,
joten ehdosta 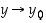 seuraa ehto
seuraa ehto 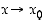 . Niinpä yllä olevan erotusosamäärän raja-arvo on
. Niinpä yllä olevan erotusosamäärän raja-arvo on 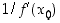 . Lauseen väite on siten todistettu.
. Lauseen väite on siten todistettu.
Kysymykseen käänteisfunktion olemassaolosta ja jatkuvuudesta palataan myöhemmin pykälässä Monotonisuus ja käänteisfunktio. Tässä vaiheessa käsitellään vain tapauksia, joissa lauseen vaatimukset (eritoten käänteisfunktion jatkuvuus) tiedetään olevan voimassa.
Funktiolla 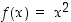 on jatkuva käänteisfunktio
on jatkuva käänteisfunktio 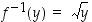 ,
kun funktioiden määrittelyt rajoitetaan väleille, joissa
,
kun funktioiden määrittelyt rajoitetaan väleille, joissa 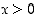 ja
ja 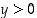 vastaavasti. Edellä olevan lauseen mukaan on
vastaavasti. Edellä olevan lauseen mukaan on
Tuloksena on siis, että neliöjuurifunktion derivaatta on
mikä on sama tulos kuin mitä esimerkissä 3.1.2 saatiin erotusosamäärän kautta.
Eräs tärkeä edellisen lauseen 3.3.9 sovellus on yleinen murtopotenssisen potenssifunktion derivaatan lauseke.
Sääntö on voimassa kaikkialla, jos 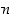 on pariton, mutta on voimassa vain positiivisille luvuille
on pariton, mutta on voimassa vain positiivisille luvuille 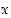 ,
jos
,
jos 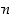 on parillinen.
on parillinen.
(b) Olkoon 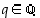 (
(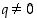 ). Silloin
). Silloin 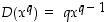 ,
kun
,
kun 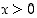 .
.
Todistus. (a) Funktion 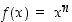 käänteiskuvaus on
käänteiskuvaus on 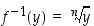 . Jos
. Jos 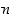 on parillinen, on määrittelyt rajattava positiivisiin lukuihin. Edellisen lauseen oletukset ovat nyt voimassa, joten
on parillinen, on määrittelyt rajattava positiivisiin lukuihin. Edellisen lauseen oletukset ovat nyt voimassa, joten
mistä väite saadaan muuttujan nimen vaihdolla.
(b) Jos 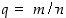 (missä
(missä 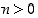 ), niin
), niin 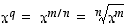 ja siten yhdistetyn funktion derivoimissäännön mukaan on
ja siten yhdistetyn funktion derivoimissäännön mukaan on
Derivoidaan seuraava lauseke osamäärän, yhdistetyn funktion ja potenssifunktion derivointisääntöjä käyttäen.
Lauseke on määritelty ja derivointi on voimassa, kun 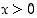 ja
ja 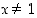 . Saatu vastaus on eräs mahdollinen sievennetty muoto − ei ole toki aina selvää, mikä olisi "sievin" muoto.
. Saatu vastaus on eräs mahdollinen sievennetty muoto − ei ole toki aina selvää, mikä olisi "sievin" muoto.
Opiskeluvideo: D5: Murtopotenssin derivointi 
