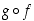 määritelty niin, että funktio
määritelty niin, että funktio 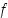 on derivoituva pisteessä
on derivoituva pisteessä 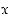 ja funktio
ja funktio 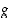 on derivoituva pisteessä
on derivoituva pisteessä 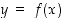 . Tällöin yhdistetty funktio
. Tällöin yhdistetty funktio 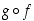 on derivoituva pisteessä
on derivoituva pisteessä 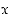 ja sen derivaatta voidaan muodostaa ns. ketjusäännöllä
ja sen derivaatta voidaan muodostaa ns. ketjusäännöllä
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tarkastellaan derivoituvista funktioista muodostettujen yhdistettyjen funktioiden derivaatan määräytymistä.
Olkoon yhdistetty funktio 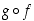 määritelty niin, että funktio
määritelty niin, että funktio 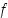 on derivoituva pisteessä
on derivoituva pisteessä 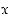 ja funktio
ja funktio 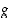 on derivoituva pisteessä
on derivoituva pisteessä 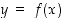 . Tällöin yhdistetty funktio
. Tällöin yhdistetty funktio 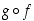 on derivoituva pisteessä
on derivoituva pisteessä 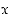 ja sen derivaatta voidaan muodostaa ns. ketjusäännöllä
ja sen derivaatta voidaan muodostaa ns. ketjusäännöllä
Todistus. On selvitettävä erotusosamäärän
raja-arvo, kun 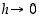 . Ensinnäkin funktion
. Ensinnäkin funktion 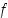 derivoituvuuden perusteella on
derivoituvuuden perusteella on
missä 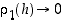 ,
kun
,
kun 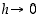 ,
ja
,
ja 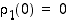 . Kun merkitään, että
. Kun merkitään, että 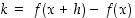 ,
niin
,
niin 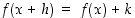 . Lisäksi funktion
. Lisäksi funktion 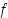 jatkuvuuden perusteella
jatkuvuuden perusteella 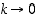 ,
kun
,
kun 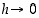 .
.
Funktion 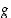 derivoituvuuden perusteella on toisaalta
derivoituvuuden perusteella on toisaalta
Edellä olevat tiedot yhdistämällä saadaan, että
Tämä osoittaa lauseen väitteen oikeaksi.
Jos funktio 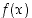 on derivoituva pisteessä
on derivoituva pisteessä 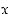 ja
ja 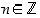 ,
,
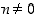 ,
niin
,
niin
Todistus. Yhdistetyn funktion ja potenssifunktion derivoimissääntöjen mukaan on
Funktion 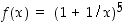 (
(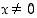 ) on yhdistetty kuvaus funktiosta
) on yhdistetty kuvaus funktiosta 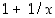 (sisäfunktio) ja potenssifunktiosta (ulkofunktio), joten sen derivaatta on
(sisäfunktio) ja potenssifunktiosta (ulkofunktio), joten sen derivaatta on
Opiskeluvideo: D4: Yhdistetyn funktion derivointi 
