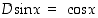Trigonometristen funktioiden derivaatat

Trigonometristen funktioiden derivaatat saadaan määrättyä selvittämällä ensin esimerkiksi sinin derivaatta erotusosamäärän kautta ja sitten muiden derivaatat käyttäen yhdistettyjen funktioiden ja osamäärien derivoimissääntöjä.

Lause 3.3.13.

Trigonometriset funktiot ovat derivoituvia määrittelyjoukoissaan ja niiden derivaatat ovat seuraavat:

(a)  ,

(b)  ,

(c)  

(d)  

Todistus. (a) Avuksi tarvitsemme seuraavan aputuloksen:

Nyt voimme laskea sinifunktion derivaatan erotusosamäärän raja-arvona seuraavasti:

(b) Kaavaa 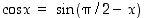käyttäen ja yhdistetyn funktion derivoimissäännöin palautetaan kosinin derivointi sinin derivointiin:

(c) Osamäärän derivoimissäännön mukaan on

(d) Kotangentin derivaatta lasketaan vastaavasti kuin tangentin derivaatta osamäärän derivoimissäännön avulla.

Esimerkki 3.3.14.

Funktio 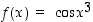on yhdistetty kuvaus funktiosta 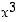(sisäfunktio) ja kosinista (ulkofunktio), joten sen derivaatta on

.

Esimerkki 3.3.15.

Funktio 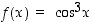on yhdistetty kuvaus kosinista (sisäfunktio) ja funktiosta 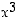(ulkofunktio), joten sen derivaatta on

.

Esimerkki 3.3.16.

Funktion derivaatta on

Opiskelutehtävä 20. (Yhdistetyn funktion derivointi)

Selvitä, miten lauseke 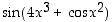muodostuu perusfunktioista (yksinkertaisemmista funktioista). Yhdistettyjen funktioiden kohdalla selvitä, mitkä ovat sisä- ja ulkofunktiot. Muodosta sitten koko lausekkeen derivaatta.

Vinkki tehtävään 20