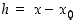 (ks. kuva 33), on
(ks. kuva 33), on 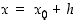 ja siten
ja siten
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Jos merkitään 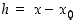 (ks. kuva 33), on
(ks. kuva 33), on 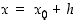 ja siten
ja siten
Tätä lauseketta (kaikkia sen muotoja) sanotaan funktion 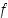 erotusosamääräksi tai Newtonin osamääräksi pisteessä
erotusosamääräksi tai Newtonin osamääräksi pisteessä 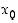 .
.
Erotusosamäärän raja-arvoja sanotaan funktion derivaatoiksi seuraavasti. Pisteen 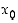 ympäristössä määritellyn funktion
ympäristössä määritellyn funktion 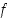 oikeanpuoleinen (op.) derivaatta pisteessä
oikeanpuoleinen (op.) derivaatta pisteessä 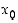 on
on
ja vasemmanpuoleinen (vp.) derivaatta pisteessä 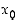 on
on
mikäli kyseiset raja-arvot ovat olemassa ja ovat äärellisiä. Mikäli molemmat raja-arvot ovat samat, yhteinen arvo on funktion 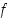 derivaatta pisteessä
derivaatta pisteessä 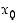 ,
merkitään
,
merkitään 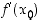 . Siten
. Siten
Koska lähestymisehdon 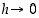 kanssa yhtäpitävää on ehto
kanssa yhtäpitävää on ehto 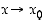 ,
voidaan kirjoittaa myös, että
,
voidaan kirjoittaa myös, että
Jos funktiolla 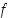 on (op./vp.) derivaatta pisteessä
on (op./vp.) derivaatta pisteessä 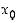 ,
sanotaan sen olevan (op./vp.) derivoituvan siinä pisteessä. Jos funktion erotusosamäärällä ei ole (op./vp.) raja-arvoa pisteessä
,
sanotaan sen olevan (op./vp.) derivoituvan siinä pisteessä. Jos funktion erotusosamäärällä ei ole (op./vp.) raja-arvoa pisteessä 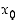 ,
on funktio (op./vp.) epäderivoituva siinä pisteessä.
,
on funktio (op./vp.) epäderivoituva siinä pisteessä.
Havainnollistus: Tangentin kulmakerroin 
Havainnollistus: Derivaatta erotusosamäärän raja-arvona 
Havainnollistus: Funktion sekantti ja tangentti 
Opiskeluvideo: D1: Derivaatta-käsite erotusosamäärän avulla 

Tarkastellaan itseisarvofunktion 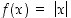 derivaattoja.
derivaattoja.
Olkoon ensin 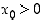 . Silloin erotusosamäärä on (kun
. Silloin erotusosamäärä on (kun 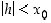 ,
jolloin
,
jolloin 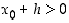 )
)
joten tämän (vakion) raja-arvona 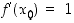 .
.
Olkoon sitten 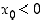 . Silloin on (kun
. Silloin on (kun 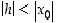 ,
jolloin
,
jolloin 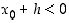 )
)
Pisteessä 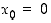 funktiolla
funktiolla 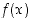 on erotusosamäärä
on erotusosamäärä
Siten oikeanpuoleinen derivaatta nollassa on
ja vastaavasti vasemmanpuoleinen derivaatta nollassa on
Funktiolla 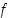 ei ole siis derivaattaa nollassa, koska toispuoleiset derivaatat ovat erisuuret.
ei ole siis derivaattaa nollassa, koska toispuoleiset derivaatat ovat erisuuret.
Opiskelutehtävä 17. (Funktion derivaatta pisteessä)
(a) Määrää derivaatta pisteessä 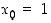 laskemalla raja-arvo
laskemalla raja-arvo
(b) Määrää derivaatta pisteessä 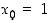 laskemalla raja-arvo
laskemalla raja-arvo
(c) Toista edelliset kohdat yleisessä pisteessä 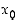 .
.
(d) Mikä on funktion 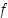 derivaattafunktio? Piirrä funktion ja derivaattafunktion kuvaajat allekkain ja tulkitse kuvat.
derivaattafunktio? Piirrä funktion ja derivaattafunktion kuvaajat allekkain ja tulkitse kuvat.
Määrätään neliöjuurifunktion 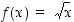 derivaatta pisteessä
derivaatta pisteessä 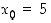 . Tarkasteltava erotuosamäärä on nyt
. Tarkasteltava erotuosamäärä on nyt
Lisäksi käyrän 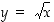 tangentin yhtälö pisteessä
tangentin yhtälö pisteessä 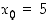 on
on
Katso kuva 34.
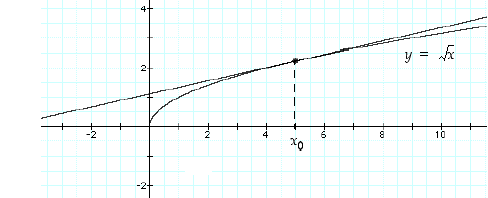
Edellä olevat tarkastelut voidaan pisteen 5 sijasta toistaa yleisessä pisteessä 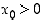 . Tulokseksi saadaan, että derivaatta on
. Tulokseksi saadaan, että derivaatta on
Opiskeluvideo: D2: Derivaatan ratkaiseminen erotusosamäärällä 

Derivaattaa ei kuitenkaan yleensä tarvitse määrätä määritelmään nojautuen erotusosamäärän raja-arvon kautta, vaan sitä varten voidaan johtaa erilaisia sääntöjä ja keinoja. Näitä johdetaan seuraavassa pykälässä. Sellaisissa erikoispisteissä, joissa yleisiä sääntöjä ei voida käyttää, derivaatta joudutaan kuitenkin määrittämään erotusosamäärän avulla.
Pykälän alussa rajoituttiin tarkastelemaan jatkuvia funktioita. Derivaatan määrittelyssä ei kuitenkaan jatkuvuutta välttämättä tarvita. Seuraava tulos osoittaa nimittäin, että funktio voi olla derivoituva vain sellaisissa pisteissä, joissa se on jatkuva.
Pisteessä 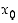 (op./vp.) derivoituva funktio
(op./vp.) derivoituva funktio 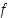 on (op./vp.) jatkuva siinä pisteessä.
on (op./vp.) jatkuva siinä pisteessä.
Todistus. Olkoon 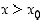 (vp. tilanne käsitellään vastaavasti). Silloin
(vp. tilanne käsitellään vastaavasti). Silloin
Funktio 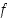 on siten oikealta jatkuva pisteessä
on siten oikealta jatkuva pisteessä 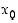 .
.
Jatkuvan funktion ei suinkaan aina tarvitse olla derivoituva. Esimerkiksi itseisarvofunktio 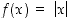 on kaikkialla jatkuva, mutta se ei ole derivoituva nollassa, sillä esimerkin 3.1.1 mukaan
on kaikkialla jatkuva, mutta se ei ole derivoituva nollassa, sillä esimerkin 3.1.1 mukaan 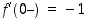 ja
ja 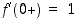 .
.
Opiskelutehtävä 18. (Derivoituvan funktion kuvaaja)
Piirrä jonkin sellaisen jatkuvan funktion  ,
,
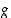 ja
ja 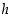 kuvaaja, joka toteuttaa annetut ehdot:
kuvaaja, joka toteuttaa annetut ehdot:
(b) 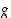 on derivoituva pisteissä
on derivoituva pisteissä 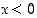 ,
,
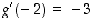 ,
,
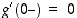 ,
,
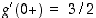 ja
ja 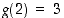 .
.
(c) 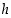 on derivoituva kaikkialla,
on derivoituva kaikkialla, 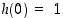 ,
,
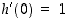 ja
ja 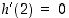 .
.
Havainnollistus: Testaa tietosi derivaatasta