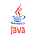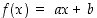 on jatkuva jokaisessa pisteessä
on jatkuva jokaisessa pisteessä 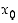 ,
joten se on jatkuva koko reaalilukujoukossa (joka on rajoittamaton väli) eli se on kaikkialla jatkuva.
,
joten se on jatkuva koko reaalilukujoukossa (joka on rajoittamaton väli) eli se on kaikkialla jatkuva.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Funktion jatkuvuus väleillä määritellään pisteittäin. Funktio on jatkuva avoimella välillä, jos se on jatkuva jokaisessa välin pisteessä. Edelleen funktio on jatkuva suljetulla tai puoliavoimella välillä, jos se on jatkuva vastaavalla avoimella välillä ja (sisäpuolelta päin) toispuoleisesti jatkuva välin päätepisteissä. Funktio on kaikkialla jatkuva, jos se on jatkuva jokaisessa reaalilukupisteessä.
Esimerkin 2.3.1 mukaan funktio 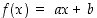 on jatkuva jokaisessa pisteessä
on jatkuva jokaisessa pisteessä 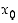 ,
joten se on jatkuva koko reaalilukujoukossa (joka on rajoittamaton väli) eli se on kaikkialla jatkuva.
,
joten se on jatkuva koko reaalilukujoukossa (joka on rajoittamaton väli) eli se on kaikkialla jatkuva.
Esimerkin 2.3.3 mukaan neliöjuurifunktio 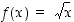 on jatkuva pisteissä
on jatkuva pisteissä 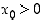 ,
joten se on jatkuva avoimella ja rajoittamattomalla välillä
,
joten se on jatkuva avoimella ja rajoittamattomalla välillä 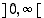 .
.
Funktio 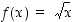 on samaisen esimerkin mukaan lisäksi oikealta jatkuva nollassa, joten kaiken kaikkiaan se on jatkuva koko määrittelyjoukossaan eli välillä
on samaisen esimerkin mukaan lisäksi oikealta jatkuva nollassa, joten kaiken kaikkiaan se on jatkuva koko määrittelyjoukossaan eli välillä 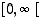 .
.
Lauseiden 2.2.11, 2.2.15 ja 2.3.6 mukaan seuraavat lauseet pätevät.
Jokainen rationaalifunktio on määrittelyjoukossaan jatkuva.
Trigonometriset funktiot ovat määrittelyjoukoissaan jatkuvia.
Jatkuvien funktioiden yhdistetyt funktiot ovat määrittelyjoukoissaan jatkuvia.
Edelleen lauseen 2.3.4 mukaan pätee seuraava.
Jatkuvista funktioista yhdistetyin funktioin ja rationaalisin lausekkein muodostetut funktiot ovat määrittelyjoukoissaan jatkuvia.
lausekkeessa funktiot 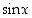 ja
ja 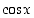 ovat kaikkialla jatkuvia, joten myös niistä rationaalisesti muodostetut funktiot
ovat kaikkialla jatkuvia, joten myös niistä rationaalisesti muodostetut funktiot 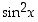 ja
ja 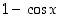 ovat kaikkialla jatkuvia. Funktio
ovat kaikkialla jatkuvia. Funktio 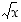 on jatkuva määrittelyjoukossaan (
on jatkuva määrittelyjoukossaan (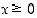 ), ks. esimerkki 2.3.3. Koko funktio
), ks. esimerkki 2.3.3. Koko funktio 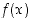 muodostuu edellä mainituista funktioista ja identtisestä funktiosta
muodostuu edellä mainituista funktioista ja identtisestä funktiosta 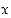 rationaalisena lausekkeena. Se on siten jatkuva niissä pisteissä, jossa se on määritelty. Määrittelyä rajaavat vain ehdot
rationaalisena lausekkeena. Se on siten jatkuva niissä pisteissä, jossa se on määritelty. Määrittelyä rajaavat vain ehdot 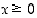 ja
ja 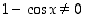 . Jälkimmäinen antaa ehdon
. Jälkimmäinen antaa ehdon 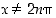 ,
,
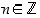 . Siten
. Siten
Määrittelyjoukko muodostuu näin ollen perättäisistä avoimista väleistä, joista ensimmäinen on 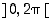 . Edellä todetun mukaan funktio
. Edellä todetun mukaan funktio 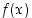 on jatkuva tässä määrittelyjoukossaan.
on jatkuva tässä määrittelyjoukossaan.
Opiskeluvideo: R7: Funktion jatkuvuus 

Jos funktio on määritelty ja jatkuva avoimella välillä, voidaan kysyä, olisiko sen määrittelyä laajennettavissa siten, että se tulisi jatkuvaksi suljetulla (tai edes puoliavoimella) välillä. Tämä onnistuu sellaisessa välin reunapisteessä, jossa funktiolla on äärellinen raja-arvo. Tällöin nimittäin voidaan funktion arvoksi siinä pisteessä määritellä kyseinen raja-arvo ja silloin funktio tulee (ainakin toispuoleisesti) jatkuvaksi siinä pisteessä.
Funktio 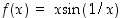 on jatkuva määrittelyjoukossaan eli kun
on jatkuva määrittelyjoukossaan eli kun 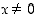 . Voiko sen määritellä nollassa niin, että se tulisi myös siinä jatkuvaksi funktioksi? Vastausta varten selvitetään, onko funktiolla
. Voiko sen määritellä nollassa niin, että se tulisi myös siinä jatkuvaksi funktioksi? Vastausta varten selvitetään, onko funktiolla 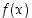 raja-arvoa nollassa. Koska
raja-arvoa nollassa. Koska
Asettamalla 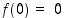 tulee funktiosta
tulee funktiosta 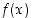 nollassa ja siten kaikkialla määritelty ja jatkuva.
nollassa ja siten kaikkialla määritelty ja jatkuva.
Opiskelutehtävä 15. (Funktion jatkuvuus ja epäjatkuvuus)
Ovatko seuraavat väittämät tosia? Myönteisessä tapauksessa perustele se, kielteisessä tapauksessa anna kumoava esimerkki.
(a) Jatkuvien funktioiden summafunktio on jatkuva.
(b) Epäjatkuvien funktioiden summafunktio on epäjatkuva.
Havainnollistus: Paloittain määritellystä funktiosta jatkuva