Harjoitustehtäviä

89.   Onko funktio

jatkuva pisteessä 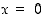? Entä muualla? (Tässä 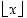on ns. lattiafunktio, jonka tulos on suurin kokonaisluku, joka on korkeintaan 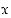; esimerkiksi 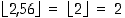ja .)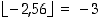

90.   Selvitä, mikä on lausekkeen

määrittelemän funktion 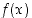määrittelyjoukko. Tutki edelleen, voidaanko funktio 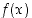lisämäärittelyllä laajentaa kaikkialla jatkuvaksi funktioksi.

91.   Miksi lauseketta 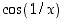ei voi jatkaa pisteessä 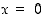jatkuvaksi funktioksi?

92.   Selvitä pätevätkö seuraavat päätelmät:

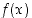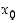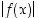(a) Jos funktio on jatkuva pisteessä , niin myös itseisarvofunktio on.

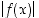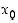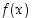(b) Jos itseisarvofunktio on jatkuva pisteessä , niin myös funktio on.

(Vihje: Erottele tapaukset 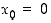ja .)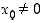

93.   Funktiosta 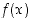tiedetään, että

Määrittele arvot 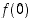ja 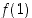niin, että funktiosta 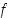tulee jatkuva pisteiss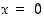ä ja 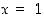. Perustele jatkuvuus.