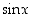 ,
,
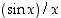 ,
,
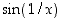 ja
ja 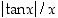 käyttäytymistä nollan lähellä. Näistä sinifunktion kuvaaja (ks. kuva 22) on säännöllisen tuntuinen nollan lähellä
käyttäytymistä nollan lähellä. Näistä sinifunktion kuvaaja (ks. kuva 22) on säännöllisen tuntuinen nollan lähellä
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tarkastellaan ensin funktioiden 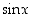 ,
,
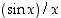 ,
,
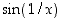 ja
ja 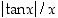 käyttäytymistä nollan lähellä. Näistä sinifunktion kuvaaja (ks. kuva 22) on säännöllisen tuntuinen nollan lähellä
käyttäytymistä nollan lähellä. Näistä sinifunktion kuvaaja (ks. kuva 22) on säännöllisen tuntuinen nollan lähellä
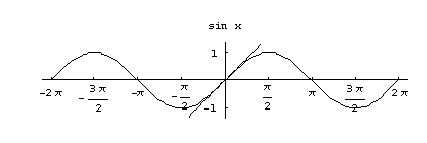
ja jos sitä tarkastellaan hyvin lähellä nollaa, se näyttää yhtyvän täysin funktioon  (ks. kuva 23).
(ks. kuva 23).
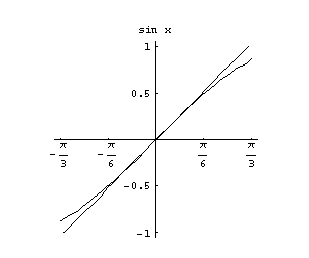
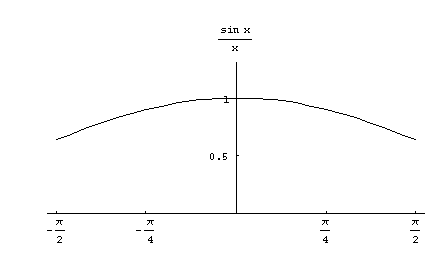
Funktiota  ei ole määritelty nollassa, mutta näyttäisi, että kuvaaja lähestyy arvoa 1 (ks. kuva 24). Onko näin todella?
ei ole määritelty nollassa, mutta näyttäisi, että kuvaaja lähestyy arvoa 1 (ks. kuva 24). Onko näin todella?
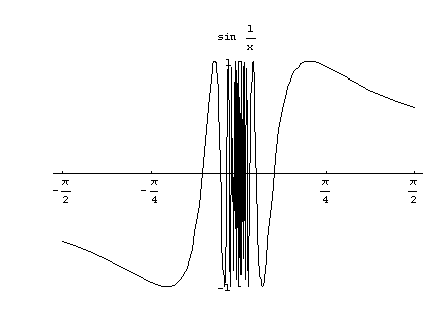
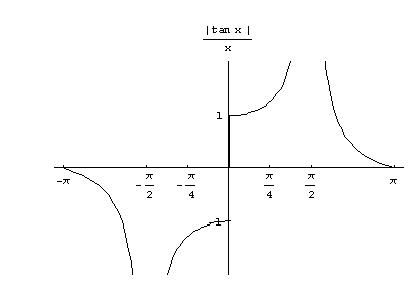
Funktiota 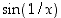 ei myöskään ole määritelty nollassa ja sen kuvaaja on sitä "suttuisempi" mitä lähempänä nollaa sitä yritetään piirtää (ks. kuva 25).
ei myöskään ole määritelty nollassa ja sen kuvaaja on sitä "suttuisempi" mitä lähempänä nollaa sitä yritetään piirtää (ks. kuva 25).
Funktiota 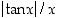 ei myöskään ole määritelty nollassa ja sen kuvaajalla on "hyppy" nollassa, ts. eri puolilta nollaa lähestyttäessä rajatulos näyttää olevan erilainen (ks. kuva 26).
ei myöskään ole määritelty nollassa ja sen kuvaajalla on "hyppy" nollassa, ts. eri puolilta nollaa lähestyttäessä rajatulos näyttää olevan erilainen (ks. kuva 26).
Mitä näille funktioille todella tapahtuu nollan lähellä? Onko se totta, miltä kuvassa näyttää? Mitä lähestymisellä oikeastaan tarkoitetaan? On siis syytä määritellä tämä lähestyminen eli ns. rajankäynti tarkemmin.
Havainnollistus: Funktion raja-arvo − johdanto 
Tarkastellaan vielä yhtä numeerista esimerkkiä.
arvoja pisteen 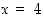 lähellä (funktiotahan ei ole määritelty kyseisessä pisteessä). Lasketaan arvoja yhä lähempänä tätä pistettä:
lähellä (funktiotahan ei ole määritelty kyseisessä pisteessä). Lasketaan arvoja yhä lähempänä tätä pistettä:

Näyttää siltä, että lähestyttäessä pistettä 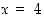 kummalta puolelta tahansa funktion arvot lähestyisivät lukua 0,08333... . Olisiko raja-arvolle löydettävissä tarkka arvo? Mikä se olisi ja miten se löydettäisiin? Vastaus annetaan esimerkissä 2.2.14.
kummalta puolelta tahansa funktion arvot lähestyisivät lukua 0,08333... . Olisiko raja-arvolle löydettävissä tarkka arvo? Mikä se olisi ja miten se löydettäisiin? Vastaus annetaan esimerkissä 2.2.14.
Seuraavassa määritellään, mitä edellä kuvatuilla lähestymisillä tarkasti ottaen tarkoitetaan.