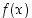 on pisteessä
on pisteessä 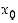 op. (vp.) raja-arvo
op. (vp.) raja-arvo 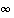 ,
jos jokaista lukua
,
jos jokaista lukua 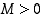 kohti on olemassa sellainen
kohti on olemassa sellainen 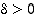 ,
että
,
että 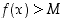 aina, kun
aina, kun 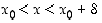 (vast.
(vast. 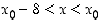 ). Tilanteita merkitään
). Tilanteita merkitään
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Edellä olevissa raja-arvotarkasteluissa on tutkittu funktion käyttäytymistä annetun reaaliluvun lähellä ja selvitetty sitä, lähestyvätkö funktion arvot jotain reaalilukua. Laajennetaan nyt tarkastelua sallimalla joko muuttujan tai funktion arvojen kasvaa tai vähentyä rajatta jompaan kumpaan äärettömyyteen päin. Jos tällaisissa tilanteissa tapahtuu funktion arvojen suppenemista, puhutaan funktion epäoleellisista raja-arvoista. Seuraavassa tarkastellaan tarkemmin eri mahdollisuuksia.
Tarkastellaan ensin tilanteita, joissa funktion arvot kasvavat tai vähenevät rajatta tarkastelupisteen lähellä. Funktiolla 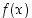 on pisteessä
on pisteessä 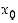 op. (vp.) raja-arvo
op. (vp.) raja-arvo 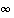 ,
jos jokaista lukua
,
jos jokaista lukua 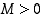 kohti on olemassa sellainen
kohti on olemassa sellainen 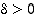 ,
että
,
että 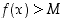 aina, kun
aina, kun 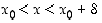 (vast.
(vast. 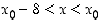 ). Tilanteita merkitään
). Tilanteita merkitään
Näissä määrittelyissä funktiosta oletetaan, että se on määritelty tarkastelupisteen 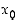 oikealla (vast. vasemmalla) puolella.
oikealla (vast. vasemmalla) puolella.
Funktiolla 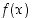 on pisteessä
on pisteessä 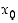 (molemminpuolinen) raja-arvo
(molemminpuolinen) raja-arvo 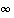 ,
jos sillä on siinä pisteessä sekä op. että vp. raja-arvo
,
jos sillä on siinä pisteessä sekä op. että vp. raja-arvo 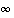 ,
merkitään
,
merkitään
Yllä olevissa tilanteissa sanotaan myös, että funktio 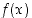 kasvaa rajatta,
kun lähestytään pistettä
kasvaa rajatta,
kun lähestytään pistettä 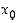 (vasemmalta, oikealta tai molemminpuolin).
(vasemmalta, oikealta tai molemminpuolin).
Vastaavasti määritellään, että funktiolla 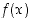 on pisteessä
on pisteessä 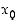 op. (vp.) raja-arvo
op. (vp.) raja-arvo 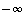 ,
jos jokaista lukua
,
jos jokaista lukua 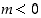 kohti on olemassa sellainen
kohti on olemassa sellainen 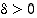 ,
että
,
että 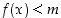 aina, kun
aina, kun 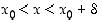 (vast.
(vast. 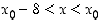 ). Funktiolla on pisteessä
). Funktiolla on pisteessä 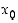 (molemminpuolinen) raja-arvo
(molemminpuolinen) raja-arvo 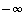 ,
jos sillä on sekä op. että vp. raja-arvo
,
jos sillä on sekä op. että vp. raja-arvo 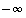 . Tilanteita merkitään
. Tilanteita merkitään
ja sanotaan, että funktio 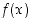 vähenee rajatta,
kun lähestytään pistettä
vähenee rajatta,
kun lähestytään pistettä 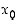 .
.
Toiseksi tarkastellaan tilanteita, joissa muuttujan 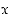 arvoja kasvatetaan tai vähennetään rajatta. Funktiolla
arvoja kasvatetaan tai vähennetään rajatta. Funktiolla 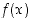 on raja-arvo
on raja-arvo 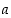 äärettömyydessä, jos jokaista lukua
äärettömyydessä, jos jokaista lukua 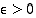 kohti on olemassa sellainen raja
kohti on olemassa sellainen raja 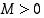 ,
että
,
että 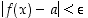 aina, kun
aina, kun 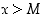 . Tilannetta merkitään
. Tilannetta merkitään
Tällaisessa tilanteessa sanotaan myös, että funktio 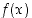 lähestyy arvoa
lähestyy arvoa 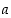 ,
kun
,
kun 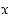 kasvaa rajatta.
kasvaa rajatta.
Vastaavasti funktiolla 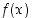 on raja-arvo
on raja-arvo 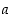 miinus-äärettömyydessä,
jos jokaista lukua
miinus-äärettömyydessä,
jos jokaista lukua 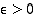 kohti on olemassa sellainen raja
kohti on olemassa sellainen raja 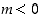 ,
että
,
että 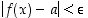 aina, kun
aina, kun 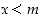 . Tilannetta merkitään
. Tilannetta merkitään
ja sanotaan, että funktio 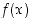 lähestyy arvoa
lähestyy arvoa 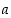 ,
kun
,
kun 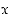 vähenee rajatta.
vähenee rajatta.
Kolmanneksi tarkastellaan tapauksia, joissa sekä funktion arvot että muuttujan arvot kasvavat tai vähenevät rajatta. Funktiolla 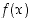 on raja-arvoa
on raja-arvoa 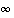 äärettömyydessä,
jos jokaista lukua
äärettömyydessä,
jos jokaista lukua 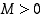 kohti on olemassa sellainen raja
kohti on olemassa sellainen raja 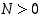 ,
että
,
että 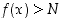 aina, kun
aina, kun 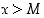 . Tilannetta merkitään
. Tilannetta merkitään
Vastaavasti määritellään raja-arvo 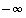 äärettömyydessä sekä raja-arvot
äärettömyydessä sekä raja-arvot 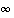 ja
ja 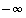 miinus-äärettömyydessä.
miinus-äärettömyydessä.
Kuten oleellisia raja-arvoja, epäoleellisiakin raja-arvoja voidaan selvittää jonojen avulla. Katso raja-arvon jonokarakterisointia lauseessa 2.2.16. Muuttujajonon tai arvojonon suppeneminen korvataan nyt toisen kasvamisella tai vähenemisellä rajatta.
Funktioilla 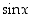 ja
ja 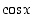 ei ole raja-arvoja äärettömyydessä eikä miinus-äärettömyydessä.
ei ole raja-arvoja äärettömyydessä eikä miinus-äärettömyydessä.
Opiskeluvideo: R2: Eripuoleiset (epäoleelliset) raja-arvot 
