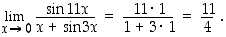Raja-arvojen rationaaliset laskusäännöt
Seuraava tulos osoittaa, että jos jossain pisteessä tiedetään useiden eri funktioiden raja-arvoja, voidaan näistä rationaalisin lausekkein muodostettujen uusien funktioiden raja-arvot päätellä rationaalisin laskutoimituksin.
Rationaalisia lausekkeita voidaan muodostaa summa-, erotus, tulo- ja osamääräfunktioin. Ne tarkoittavat seuraavien funktioiden muodostamistapojen toistuvaa käyttöä. Kahden funktion 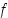 ja
ja 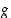 summafunktio
summafunktio 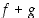 määritellään määrittelyjoukkojen leikkausjoukossa
määritellään määrittelyjoukkojen leikkausjoukossa 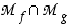 lausekkeella
lausekkeella 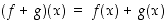 . Vastaavasti määritellään erotus
. Vastaavasti määritellään erotus 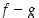 ,
tulo
,
tulo 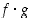 ja osamäärä
ja osamäärä 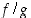 . Osamääräfunktion kohdalla on lisäksi jätettävä mahdolliset nimittäjän nollakohdat pois määrittelyjoukosta.
. Osamääräfunktion kohdalla on lisäksi jätettävä mahdolliset nimittäjän nollakohdat pois määrittelyjoukosta.
Lause 2.2.8. (Raja-arvojen rationaaliset laskusäännöt)
Jos funktioilla 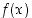 ja
ja 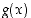 ovat (op./vp./mp.) raja-arvot olemassa jossain pisteessä, niin (op./vp./mp.) raja-arvoille ko. pisteessä on
ovat (op./vp./mp.) raja-arvot olemassa jossain pisteessä, niin (op./vp./mp.) raja-arvoille ko. pisteessä on
(a) 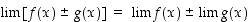 ,
,
(b) 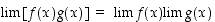 ,
,
(c) 
Todistus. Tulokset voidaan johtaa suoraan raja-arvojen määritelmistä. Käydään tässä läpi vain ensimmäisen kohdan summaa koskeva väite op. raja-arvoille. Muut kohdat voidaan todistaa samaan tapaan kuin jonoja koskevat säännöt lauseessa 2.1.7.
Olkoot
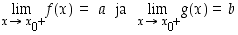
sekä olkoon 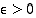 . Silloin jollekin
. Silloin jollekin 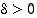 on
on
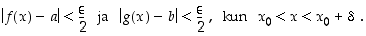
Tällöin
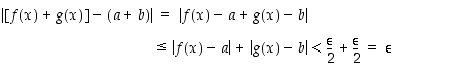
aina kun 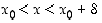 . Siten
. Siten
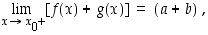
kuten väitettiin.

Esimerkki 2.2.9.
Selvitetään onko raja-arvoa
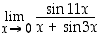
olemassa. Pyritään käyttämään esimerkin 2.2.6 raja-arvoa hyväksi. Kun 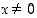 ,
voidaan tarkasteltavaa lauseketta muokata seuraavasti:
,
voidaan tarkasteltavaa lauseketta muokata seuraavasti:
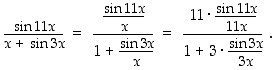
Tässä suhde 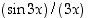 on muotoa
on muotoa 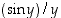 ,
missä
,
missä 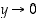 (kun
(kun 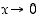 ). Esimerkin 2.2.6 mukaan tämän raja-arvo on 1. Samasta syystä lausekkeen
). Esimerkin 2.2.6 mukaan tämän raja-arvo on 1. Samasta syystä lausekkeen 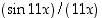 raja-arvo on 1. Tulokseksi saadaan raja-arvojen rationaalisia laskusääntöjä käyttäen, että
raja-arvo on 1. Tulokseksi saadaan raja-arvojen rationaalisia laskusääntöjä käyttäen, että
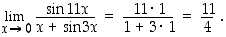

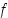 ja
ja 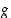 summafunktio
summafunktio 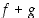 määritellään määrittelyjoukkojen leikkausjoukossa
määritellään määrittelyjoukkojen leikkausjoukossa 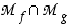 lausekkeella
lausekkeella 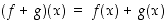 . Vastaavasti määritellään erotus
. Vastaavasti määritellään erotus 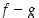 ,
tulo
,
tulo 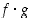 ja osamäärä
ja osamäärä 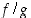 . Osamääräfunktion kohdalla on lisäksi jätettävä mahdolliset nimittäjän nollakohdat pois määrittelyjoukosta.
. Osamääräfunktion kohdalla on lisäksi jätettävä mahdolliset nimittäjän nollakohdat pois määrittelyjoukosta. 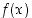 ja
ja 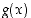 ovat (op./vp./mp.) raja-arvot olemassa jossain pisteessä, niin (op./vp./mp.) raja-arvoille ko. pisteessä on
ovat (op./vp./mp.) raja-arvot olemassa jossain pisteessä, niin (op./vp./mp.) raja-arvoille ko. pisteessä on 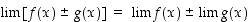 ,
,
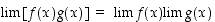 ,
,

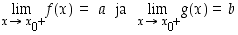
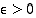 . Silloin jollekin
. Silloin jollekin 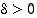 on
on 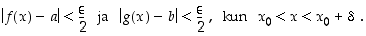
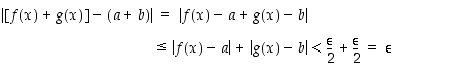
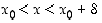 . Siten
. Siten 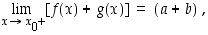

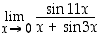
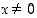 ,
voidaan tarkasteltavaa lauseketta muokata seuraavasti:
,
voidaan tarkasteltavaa lauseketta muokata seuraavasti: 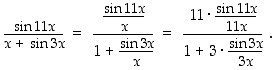
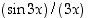 on muotoa
on muotoa 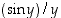 ,
missä
,
missä 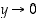 (kun
(kun 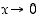 ). Esimerkin
). Esimerkin 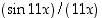 raja-arvo on 1. Tulokseksi saadaan raja-arvojen rationaalisia laskusääntöjä käyttäen, että
raja-arvo on 1. Tulokseksi saadaan raja-arvojen rationaalisia laskusääntöjä käyttäen, että