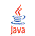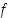 ,
,
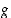 ja
ja 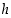 pätevät jollain välillä
pätevät jollain välillä 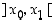 epäyhtälöt
epäyhtälöt 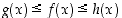 ja jos
ja jos
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Seuraava lause on usein kätevä raja-arvojen määräämisessä.
Lause 2.2.4. (Voileipälause eli kuristuslause)
Jos funktioille 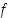 ,
,
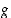 ja
ja 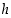 pätevät jollain välillä
pätevät jollain välillä 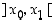 epäyhtälöt
epäyhtälöt 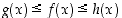 ja jos
ja jos
Vastaava tulos pätee vp. raja-arvoille.
Todistus. Raja-arvojen olemassaolon mukaan annetulle 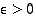 on olemassa
on olemassa 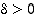 siten, että
siten, että
Silloin myös 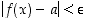 ,
mikä osoittaakin väitteen oikeaksi.
,
mikä osoittaakin väitteen oikeaksi.
Edellä olevaa lausetta voidaan käyttää sellaisessa tilanteessa, jossa itse funktion lauseke on hankalasti käsiteltävä, mutta jossa sitä voidaan lähellä tarkastelupistettä arvioida sekä ylhäältä että alhaalta funktioilla, joiden lauseke on mahdollisesti helpompi käsitellä ja joiden raja-arvojen tiedetään olevan samat.
Huomaa, että lauseketta ei ole määritelty nollassa.
Tarkastellaan ensin op. raja-arvoa. Voimme olettaa sitä varten, että 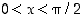 . Tarkastellaan kuvaa 28.
. Tarkastellaan kuvaa 28.
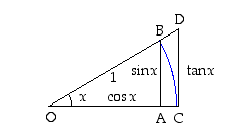
Yksikköympyrän sektorin OCB ala on
ja toisaalta kolmion OCD ala on
Koska näistä sektori on alaltaan pienempi kuin kolmio, saadaan epäyhtälö
Toisaalta positiivisilla arvoilla on 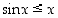 ,
joten
,
joten 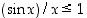 . Yhdistämällä epäyhtälöt saadaan, että
. Yhdistämällä epäyhtälöt saadaan, että
Koska 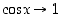 ,
kun
,
kun 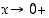 (trigonometristen funktioiden rajakäyttäytyminen perustellaan tosin yleisemmin vasta lauseessa 2.2.15), niin kuristuslauseen mukaan myös
(trigonometristen funktioiden rajakäyttäytyminen perustellaan tosin yleisemmin vasta lauseessa 2.2.15), niin kuristuslauseen mukaan myös 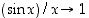 ,
kun
,
kun 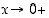 .
.
Vp. raja-arvo voidaan nyt päätellä edellä olevan avulla:
Toispuoleiset raja-arvot ovat siten samat.
Havainnollistus: Lausekkeen sin(x) / x raja-arvo nollassa