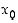 ja oletetaan ensin, että funktio
ja oletetaan ensin, että funktio 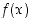 on määritelty jollain välillä
on määritelty jollain välillä 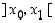 ,
missä
,
missä 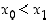 . Funktiolla
. Funktiolla 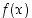 on pisteessä
on pisteessä 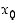 oikeanpuoleinen (op.) raja-arvo
oikeanpuoleinen (op.) raja-arvo 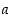 ,
jos jokaista lukua
,
jos jokaista lukua 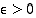 kohti on olemassa sellainen luku
kohti on olemassa sellainen luku 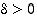 ,
että
,
että
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Tarkastellaan pistettä 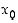 ja oletetaan ensin, että funktio
ja oletetaan ensin, että funktio 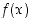 on määritelty jollain välillä
on määritelty jollain välillä 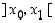 ,
missä
,
missä 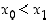 . Funktiolla
. Funktiolla 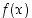 on pisteessä
on pisteessä 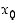 oikeanpuoleinen (op.) raja-arvo
oikeanpuoleinen (op.) raja-arvo 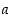 ,
jos jokaista lukua
,
jos jokaista lukua 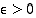 kohti on olemassa sellainen luku
kohti on olemassa sellainen luku 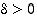 ,
että
,
että
Tässä tilanteessa merkitään, että
Kun raja-arvo on olemassa, se tarkoittaa, että mille tahansa funktion arvojen 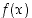 tarkkuudelle
tarkkuudelle 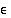 eli niiden erolle arvosta
eli niiden erolle arvosta 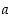 löytyy sellainen muuttujan
löytyy sellainen muuttujan 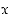 tarkkuus
tarkkuus 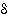 ,
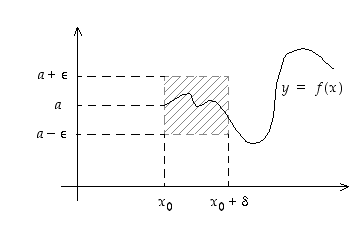
että funktion arvot tämän muuttujatarkkuuden jälkeen toteuttavat aina vaaditun tarkkuuden. Graafisesti tämä merkitsee sitä, että lähellä pistettä
,
että funktion arvot tämän muuttujatarkkuuden jälkeen toteuttavat aina vaaditun tarkkuuden. Graafisesti tämä merkitsee sitä, että lähellä pistettä 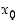 funktion kuvaaja on suorakaiteen
funktion kuvaaja on suorakaiteen
sisällä (ks. kuva 27).
Vastaavasti funktiolla 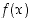 ,
joka on määritelty jollain välillä
,
joka on määritelty jollain välillä 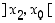 ,
missä
,
missä 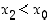 ,
on pisteessä
,
on pisteessä 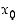 vasemmanpuoleinen (vp.) raja-arvo
vasemmanpuoleinen (vp.) raja-arvo 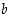 ,
jos jokaista lukua
,
jos jokaista lukua 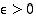 kohti on olemassa sellainen luku
kohti on olemassa sellainen luku 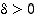 ,
että
,
että
Tässä tilanteessa merkitään, että
Huomaa, että kummassakaan määrittelyssä funktion 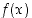 arvoa pisteessä
arvoa pisteessä 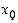 ei tarvita, joten funktion ei tarvitse olla määritelty siinä pisteessä, jossa raja-arvo halutaan määrätä. Riittää, että se on määritelty sillä puolella tätä pistettä, jolta raja-arvoa määrätään.
ei tarvita, joten funktion ei tarvitse olla määritelty siinä pisteessä, jossa raja-arvo halutaan määrätä. Riittää, että se on määritelty sillä puolella tätä pistettä, jolta raja-arvoa määrätään.
Havainnollistus: Raja-arvo-esimerkki 
Funktiota 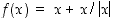 ei ole määritelty nollassa, mutta kylläkin mielivaltaisen lähellä sitä, joten voimme katsoa, onko sillä (toispuoleisia) raja-arvoja siinä pisteessä. Nähdään, että
ei ole määritelty nollassa, mutta kylläkin mielivaltaisen lähellä sitä, joten voimme katsoa, onko sillä (toispuoleisia) raja-arvoja siinä pisteessä. Nähdään, että 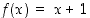 ,
kun
,
kun 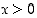 ,
ja
,
ja 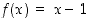 ,
kun
,
kun 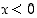 . Siten selvästi
. Siten selvästi 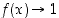 ,
kun
,
kun 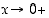 ,
ja
,
ja 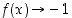 ,
kun
,
kun 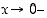 . Toisin sanoen
. Toisin sanoen
Jos funktiolla on jossain pisteessä op./vp. raja-arvo, se on yksikäsitteisesti määrätty.
Todistus. Oletetaan, että pisteessä 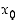 funktiolla
funktiolla 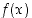 on kaksi eri op. raja-arvoa, toisin sanoen
on kaksi eri op. raja-arvoa, toisin sanoen
missä 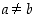 . Valitaan raja-arvon määritelmässä
. Valitaan raja-arvon määritelmässä 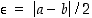 ,
jolloin on olemassa sellainen luku
,
jolloin on olemassa sellainen luku 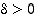 ,
että
,
että
aina kun 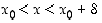 . Mutta silloin kolmioepäyhtälön mukaan olisi
. Mutta silloin kolmioepäyhtälön mukaan olisi
mikä on ristiriita. Ei siis ole olemassa kahta eri op. raja-arvoa.
Samaan tapaan päätellään vp. raja-arvon yksikäsitteisyys.