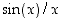raja-arvo kohdassa nolla muodostuu. Pistettä B voi liikuttaa yksikköympyrän kaarella.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Sivun tarkoituksena on visualisoida sitä, kuinka funktion 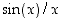raja-arvo kohdassa nolla muodostuu. Pistettä B voi liikuttaa yksikköympyrän kaarella.
Tehtävät löytyvät kuvan jälkeen.
Pistettä B liikutettaessa muuttuu kulman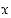 
suuruus. Trigonometrian avulla voidaan kolmioiden OAB ja OCD sekä sektorin OCB ala ilmaista kulman 
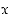funktiona, kuten seuraavassa opastetaan.
(Vastaukset saa näkyviin laittamalla kyseistä tehtäväkohtaa vastaava liukukytkin asentoon 'näytä')
2. Millaisen epäyhtälön saat vertaamalla näitä aloja toisiinsa? (Vastauksen löydät ylhäältä 'Alojen suuruusjärjestys' -kohdasta siirtämällä liukukytkin näytä-asentoon)
3. Kuinka tästä epäyhtälöstä voidaan johtaa funktiolle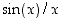 
raja-arvo kohdassa nolla? (Vihje: Muokkaa epäyhtälöä niin, että saat keskimmäiseksi lausekkeeksi 
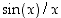tai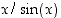 
. Tämän jälkeen kuristuslauseesta on apua!)
Tekstisijainti: Lausekkeen sin(x) / x raja-arvo nollassa