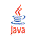Napakoordinaattiesitys
Kompleksiluvut 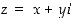 voidaan havainnollistaa ajattelemalla niitä kaksiulotteisen vektoriavaruuden eli tason alkioina. Silloin kompleksilukujen yhteenlasku on samanlainen kuin vektoreiden yhteenlasku (ajatellen, että koordinaatiston kantavektoreina ovat luvut 1 ja
voidaan havainnollistaa ajattelemalla niitä kaksiulotteisen vektoriavaruuden eli tason alkioina. Silloin kompleksilukujen yhteenlasku on samanlainen kuin vektoreiden yhteenlasku (ajatellen, että koordinaatiston kantavektoreina ovat luvut 1 ja 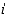 ).
).
Ajatellaan nyt, että tason pisteeseen 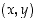 siirrytään vaaka- ja pystysuuntien sijasta suunta ja etäisyys -periaatteella (ks. kuva 20).
siirrytään vaaka- ja pystysuuntien sijasta suunta ja etäisyys -periaatteella (ks. kuva 20).
Kuva 20.
Pisteen 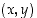 etäisyys origosta on
etäisyys origosta on 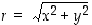 ja kulma
ja kulma 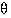 olkoon säteen ja reaaliakselin väliin jäävä kulma. Kompleksiluvun
olkoon säteen ja reaaliakselin väliin jäävä kulma. Kompleksiluvun 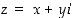 itseisarvo eli moduli on luku
itseisarvo eli moduli on luku
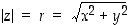
ja sen argumentti on 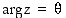 . Argumentille sovitaan yleensä, että
. Argumentille sovitaan yleensä, että 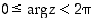 . Se määräytyy ehdoista
. Se määräytyy ehdoista
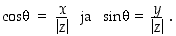
Ehdoista 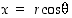 ja
ja 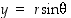 ,
missä
,
missä 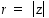 ,
saadaan esitys
,
saadaan esitys
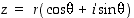 .
.
Tätä esitystä sanotaan kompleksiluvun 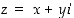 napakoordinaattiesitykseksi. Viimeistään tämän esityksen myötä kompleksiluvut ovat muuttuneet kuvitteellisista konkreeteiksi!
napakoordinaattiesitykseksi. Viimeistään tämän esityksen myötä kompleksiluvut ovat muuttuneet kuvitteellisista konkreeteiksi!
Esimerkki 1.7.2.
Minkä kompleksiluvun itseisarvo on 4 ja argumentti 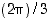 ? Vastauksena on luku
? Vastauksena on luku
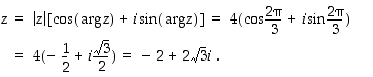

Esimerkki 1.7.3.
Kompleksiluvun 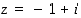 moduli on
moduli on 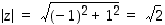 . Ehdoista
. Ehdoista
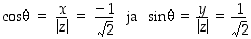
nähdään, että sen argumentti on 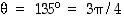 .
.
Argumentin voi päätellä myös pelkästä sinin tai kosinin arvosta, kunhan huomioi lisäksi sen, missä neljänneksessä kompleksiluvun on oltava. Tässä tapauksessa reaaliosa on negatiivinen ja imaginaariosa positiivinen, joten kompleksiluku sijaitsee toisessa neljänneksessä.

Seuraavien lauseiden 1.7.4−1.7.6 todistukset ovat suoraviivaisia laskuja ja ne jätetäänkin lukijalle harjoitustehtäviksi. (Ensimmäisen osalta ks. tehtävä 59.)
Lause 1.7.4.
Kompleksiluvuille 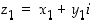 ja
ja 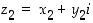 pätevät seuraavat.
pätevät seuraavat.
(a) 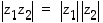 ,
,
(b) 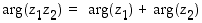 (
(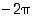 ,
jos summa on yli
,
jos summa on yli 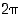 ),
),
(c) 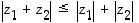 (Kolmioepäyhtälö).
(Kolmioepäyhtälö).
Soveltamalla induktiivisesti edellä olevaa tulosta kun 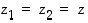 saadaan seuraava tulos (ks. harjoitustehtävä 60).
saadaan seuraava tulos (ks. harjoitustehtävä 60).
Lause 1.7.5.
Napakoordinaattimuodossa esitetylle kompleksiluvulle 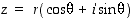 on
on
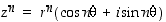 kaikille
kaikille 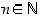 (de Moivren kaava).
(de Moivren kaava).
Jos napakoordinaattimuotoista kompleksilukua merkittäisiin vaikkapa 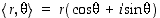 ,
ilmaisisi lauseen 1.7.4 kaksi ensimmäistä kohtaa sen, että kompleksilukujen kertolaskusääntö olisi yksinkertaisesti
,
ilmaisisi lauseen 1.7.4 kaksi ensimmäistä kohtaa sen, että kompleksilukujen kertolaskusääntö olisi yksinkertaisesti 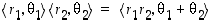 . De Moivren kaava taas olisi muotoa
. De Moivren kaava taas olisi muotoa 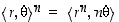 .
.
Seuraavat muokkaussäännöt ovat suoraviivaisia todistaa laskemalla (ks. harjoitustehtävä 61).
Lause 1.7.6.
Kompleksiluvulle 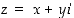 pätevät seuraavat.
pätevät seuraavat.
(a) 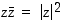 ,
,
(b) 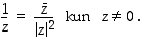
Opiskelutehtävä 9. (Kompleksilukujen aritmetiikkaa)
Laske kompleksiluvuille 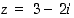 ja
ja 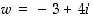 kompleksiluvut
kompleksiluvut 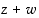 ,
,
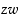 ,
,
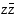 ,
,
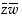 ,
,
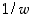 ja
ja 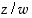 sekä reaaliluvut
sekä reaaliluvut 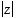 ,
,
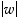 ja
ja 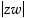 .
.
Vinkki tehtävään 9
Opiskelutehtävä 10. (Kompleksilukujen napakoordinaattiesitys)
Olkoon 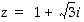 .
.
(a) Määrää luvulle 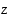 napakoordinaattiesitys.
napakoordinaattiesitys.
(b) Laske 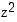 ,
,
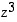 ,
,
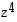 ,
.... Mitä huomaat?
,
.... Mitä huomaat?
(c) Määrää 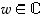 niin, että
niin, että 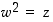 .
.
Vinkki tehtävään 10
Havainnollistus: Kompleksilukujen laskutoimitukset 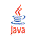
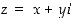 voidaan havainnollistaa ajattelemalla niitä kaksiulotteisen vektoriavaruuden eli tason alkioina. Silloin kompleksilukujen yhteenlasku on samanlainen kuin vektoreiden yhteenlasku (ajatellen, että koordinaatiston kantavektoreina ovat luvut 1 ja
voidaan havainnollistaa ajattelemalla niitä kaksiulotteisen vektoriavaruuden eli tason alkioina. Silloin kompleksilukujen yhteenlasku on samanlainen kuin vektoreiden yhteenlasku (ajatellen, että koordinaatiston kantavektoreina ovat luvut 1 ja 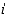 ).
). 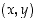 siirrytään vaaka- ja pystysuuntien sijasta suunta ja etäisyys -periaatteella (ks. kuva
siirrytään vaaka- ja pystysuuntien sijasta suunta ja etäisyys -periaatteella (ks. kuva 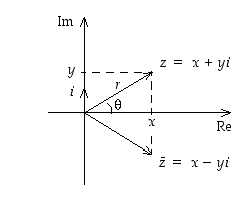
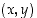 etäisyys origosta on
etäisyys origosta on 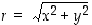 ja kulma
ja kulma 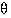 olkoon säteen ja reaaliakselin väliin jäävä kulma. Kompleksiluvun
olkoon säteen ja reaaliakselin väliin jäävä kulma. Kompleksiluvun 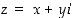 itseisarvo
itseisarvo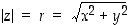
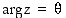 . Argumentille sovitaan yleensä, että
. Argumentille sovitaan yleensä, että 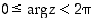 . Se määräytyy ehdoista
. Se määräytyy ehdoista 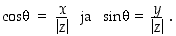
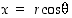 ja
ja 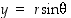 ,
missä
,
missä 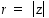 ,
saadaan esitys
,
saadaan esitys 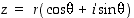 .
. 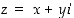 napakoordinaattiesitykseksi
napakoordinaattiesitykseksi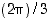 ? Vastauksena on luku
? Vastauksena on luku 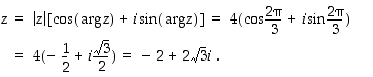

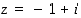 moduli on
moduli on 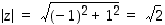 . Ehdoista
. Ehdoista 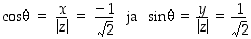
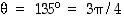 .
. 
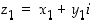 ja
ja 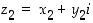 pätevät seuraavat.
pätevät seuraavat. 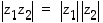 ,
,
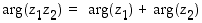 (
(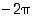 ,
jos summa on yli
,
jos summa on yli 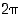 ),
), 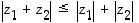
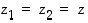 saadaan seuraava tulos (ks. harjoitustehtävä
saadaan seuraava tulos (ks. harjoitustehtävä 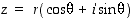 on
on 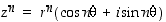 kaikille
kaikille 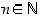 (de Moivren kaava
(de Moivren kaava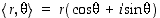 ,
ilmaisisi lauseen
,
ilmaisisi lauseen 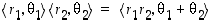 . De Moivren kaava taas olisi muotoa
. De Moivren kaava taas olisi muotoa 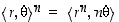 .
. 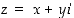 pätevät seuraavat.
pätevät seuraavat. 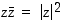 ,
,
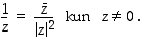
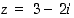 ja
ja 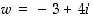 kompleksiluvut
kompleksiluvut 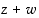 ,
,
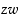 ,
,
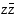 ,
,
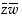 ,
,
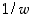 ja
ja 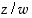 sekä reaaliluvut
sekä reaaliluvut 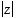 ,
,
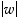 ja
ja 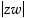 .
. 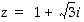 .
. 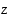 napakoordinaattiesitys.
napakoordinaattiesitys. 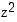 ,
,
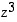 ,
,
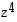 ,
.... Mitä huomaat?
,
.... Mitä huomaat? 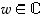 niin, että
niin, että 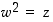 .
.