 on
on
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
50. Osoita, että kompleksiluvulle 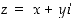 on
on
51. Muodosta osamäärän 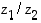 reaali- ja imaginaariosat, kun
reaali- ja imaginaariosat, kun 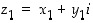 ja
ja 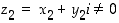 .
.
52. Kerro kompleksiluvulla 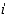 muita kompleksilukuja (esimerkiksi
muita kompleksilukuja (esimerkiksi 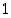 ,
,
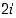 ,
,
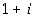 ,
,
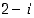 ja
ja 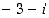 ) ja päättele, miten tämä kertominen muuntaa lukuja kompleksitasossa.
) ja päättele, miten tämä kertominen muuntaa lukuja kompleksitasossa.
53. Sama kuin edellinen tehtävä, mutta kertojana on nyt luku 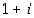 .
.
54. Osoita, että 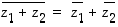 ja
ja 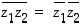 ,
kun
,
kun 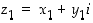 ja
ja 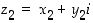 .
.
reaalikertoiminen polynomi, jolla on kompleksinen juuri 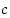 . Perustele, miksi myös liittoluku
. Perustele, miksi myös liittoluku 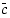 on sen juuri.
on sen juuri.
57. Onko yhtälöllä (a) 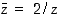 ,
(b)
,
(b) 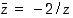 kompleksilukuratkaisuja
kompleksilukuratkaisuja 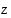 ?
?
58. Laske 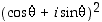 kahdella eri tavalla (korottamalla potenssiin ja de Moivren kaavalla) ja päättele tuloksista sinin ja kosinin tuplakulmasäännöt.
kahdella eri tavalla (korottamalla potenssiin ja de Moivren kaavalla) ja päättele tuloksista sinin ja kosinin tuplakulmasäännöt.
59. Osoita, että kompleksiluvuille 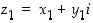 ja
ja 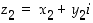 pätevät seuraavat:
pätevät seuraavat:
60. Oletetaan, että kompleksiluvulle 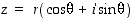 on
on 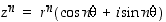 jollekin
jollekin 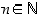 . Osoita, että vastaava kaava pätee myös potenssille
. Osoita, että vastaava kaava pätee myös potenssille 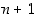 . (Tämä todistaa oleellisesti de Moivren kaavan, ks. lause 1.7.5.)
. (Tämä todistaa oleellisesti de Moivren kaavan, ks. lause 1.7.5.)
61. Osoita, että kompleksiluvulle 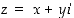 pätevät seuraavat:
pätevät seuraavat:
(a) Määrää luvun 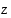 napakoordinaattiesitys.
napakoordinaattiesitys.
(c) Määrää kompleksiluku 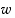 siten, että
siten, että 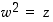 .
.
63. Olkoon 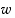 kompleksiluku, jonka moduli on yksi ja argumentti on
kompleksiluku, jonka moduli on yksi ja argumentti on 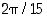 .
.
(a) Osoita, että 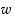 toteuttaa yhtälön
toteuttaa yhtälön 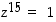 .
.
(b) Osoita, että myös 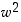 ,
,
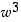 ,
...,
,
..., 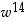 toteuttavat kaikki yhtälön
toteuttavat kaikki yhtälön 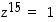 .
.
(c) Sijoita 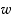 ,
,
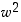 ,
,
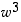 ,
...,
,
..., 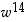 kompleksitasoon. Mitä huomaat?
kompleksitasoon. Mitä huomaat?
64. Ratkaise ns. Cardanon probleema: Kahden luvun summa on 10 ja tulo 40. Mitkä luvut ovat?
65. Määrää vakio 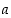 niin, että
niin, että 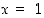 on yhtälön
on yhtälön 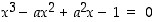 ratkaisu. Mitkä ovat tällöin muut ratkaisut? Määrää myös kompleksilukuratkaisut.
ratkaisu. Mitkä ovat tällöin muut ratkaisut? Määrää myös kompleksilukuratkaisut.
67. Esitä yhtälön 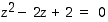 ratkaisut napakoordinaattimuodossa.
ratkaisut napakoordinaattimuodossa.