Abstrakti määrittely
Reaalilukujen joukossa yhtälöllä 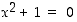 ei ole ratkaisua. Olisiko olemassa sellaista lukujoukkoa, jossa ratkaisu löytyisi? Kuvitellaan, että sellainen joukko olisi olemassa, ja ajatellaan, että jokin kuvitteellinen (imaginaarinen) "luku"
ei ole ratkaisua. Olisiko olemassa sellaista lukujoukkoa, jossa ratkaisu löytyisi? Kuvitellaan, että sellainen joukko olisi olemassa, ja ajatellaan, että jokin kuvitteellinen (imaginaarinen) "luku" 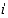 olisi yksi edellä olevan yhtälön ratkaisu. Halutaan edelleen, että samat yhteen- ja kertolaskuominaisuudet kuin reaaliluvuilla olisivat voimassa myös tässä kuvitellussa laajemmassa joukossa. Silloin siinä joukossa olisi oltava myös mm. kaikki muotoa
olisi yksi edellä olevan yhtälön ratkaisu. Halutaan edelleen, että samat yhteen- ja kertolaskuominaisuudet kuin reaaliluvuilla olisivat voimassa myös tässä kuvitellussa laajemmassa joukossa. Silloin siinä joukossa olisi oltava myös mm. kaikki muotoa 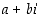 olevat luvut, joissa
olevat luvut, joissa 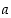 ja
ja 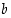 ovat mitä tahansa reaalilukuja. Edelleen kaikki näiden summat, erotukset, tulot ja osamäärät. Muodostetaan kahden tällaisen luvun
ovat mitä tahansa reaalilukuja. Edelleen kaikki näiden summat, erotukset, tulot ja osamäärät. Muodostetaan kahden tällaisen luvun 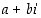 ja
ja 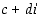 summa ja tulo. Oletamme siis, että "luvulla"
summa ja tulo. Oletamme siis, että "luvulla" 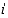 voidaan laskea kuin reaalilukumuuttujalla yleensäkin. Silloin summalle saadaan
voidaan laskea kuin reaalilukumuuttujalla yleensäkin. Silloin summalle saadaan
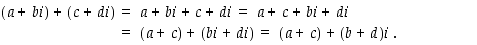
ja edelleen se huomioiden, että 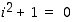 eli
eli 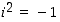 ,
saadaan tulolle vastaavasti
,
saadaan tulolle vastaavasti
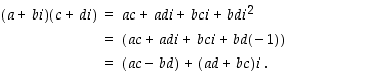
Tuloksena on, että sekä summa että tulo ovat edelleen saman muotoisia lausekkeita.
Edellä olevan johdattelun perusteella määrittelemme, että kompleksiluvut muodostuvat joukosta
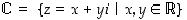 ,
,
jonka alkioiden 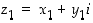 ja
ja 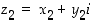 yhteen- ja kertolasku määritellään säännöillä
yhteen- ja kertolasku määritellään säännöillä
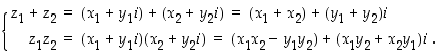
Kompleksiluvulle 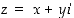 on
on 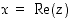 sen reaaliosa ja
sen reaaliosa ja 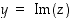 sen imaginaariosa. Lukua
sen imaginaariosa. Lukua 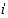 sanotaan imaginaariyksiköksi. Jos kompleksiluvun imaginaariosa on nolla, on se reaalinen luku. Jokainen reaaliluku
sanotaan imaginaariyksiköksi. Jos kompleksiluvun imaginaariosa on nolla, on se reaalinen luku. Jokainen reaaliluku 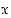 on siis myös kompleksiluku:
on siis myös kompleksiluku: 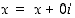 . Kompleksiluku on taas aito kompleksiluku, jos sen imaginaariosa ei ole nolla. Kompleksiluku on nolla vain, jos sekä reaaliosa että imaginaariosa ovat nollia, merkitään
. Kompleksiluku on taas aito kompleksiluku, jos sen imaginaariosa ei ole nolla. Kompleksiluku on nolla vain, jos sekä reaaliosa että imaginaariosa ovat nollia, merkitään 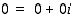 .
.
Edellä olevan mukaan kompleksilukujen summat ja tulot ovat edelleen kompleksilukuja. Seuraavan tuloksen mukaan myös kompleksilukujen vastaluvut ja käänteisluvut ovat edelleen kompleksilukuja. Sama pätee siten yleisemmin myös erotuksille ja osamäärille.
Lause 1.7.1.
Kompleksiluvun 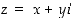 vastaluku ja käänteisluku ovat seuraavat:
vastaluku ja käänteisluku ovat seuraavat:
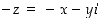 ,
ja
,
ja
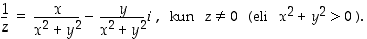
Todistus. On osoitettava, että (a) 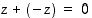 ja (b)
ja (b) 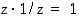 . Näistä kohta (a) on ilmeinen ja kohta (b) jätetään harjoitustehtäväksi (tehtävä 50).
. Näistä kohta (a) on ilmeinen ja kohta (b) jätetään harjoitustehtäväksi (tehtävä 50).

Kompleksilukujen määrittelyn ja edellisen tuloksen jälkeen voidaan todeta yhteenvetona, että kompleksiluvuilla on samat yhteen- ja kertolaskuominaisuudet kuin rationaali- ja reaaliluvuilla (ks. Rationaali- ja reaalilukujen aksioomat). Kompleksiluvuille ei voi kuitenkaan määritellä mitään sellaista järjestystä (eikä siten positiivisuutta tai negatiivisuuttakaan), että niille olisivat voimassa samat järjestyssäännöt kuin reaaliluvuille.
Kompleksilukujen tasotulkintaan perustuu seuraavaa nimitys. Kompleksilukua 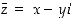 sanotaan luvun
sanotaan luvun 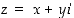 liittoluvuksi eli konjugaatiksi (ks. kuva 20). Liittoluvun muodostamiselle pätee, että
liittoluvuksi eli konjugaatiksi (ks. kuva 20). Liittoluvun muodostamiselle pätee, että
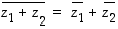 ja
ja 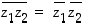 ,
,
kun 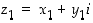 ja
ja 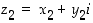 . Näiden sääntöjen todennus jätetään harjoitustehtäväksi (tehtävä 54).
. Näiden sääntöjen todennus jätetään harjoitustehtäväksi (tehtävä 54).
Havainnollistus: Kompleksilukujen yhteenlasku 
Havainnollistus: Kompleksilukujen vähennyslasku 
Laskentapohja: Kompleksilukujen summa 
Laskentapohja: Kompleksilukujen tulo 
Laskentapohja: Kompleksilukujen jakolasku 
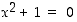 ei ole ratkaisua. Olisiko olemassa sellaista lukujoukkoa, jossa ratkaisu löytyisi? Kuvitellaan, että sellainen joukko olisi olemassa, ja ajatellaan, että jokin kuvitteellinen (imaginaarinen) "luku"
ei ole ratkaisua. Olisiko olemassa sellaista lukujoukkoa, jossa ratkaisu löytyisi? Kuvitellaan, että sellainen joukko olisi olemassa, ja ajatellaan, että jokin kuvitteellinen (imaginaarinen) "luku" 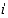 olisi yksi edellä olevan yhtälön ratkaisu. Halutaan edelleen, että samat yhteen- ja kertolaskuominaisuudet kuin reaaliluvuilla olisivat voimassa myös tässä kuvitellussa laajemmassa joukossa. Silloin siinä joukossa olisi oltava myös mm. kaikki muotoa
olisi yksi edellä olevan yhtälön ratkaisu. Halutaan edelleen, että samat yhteen- ja kertolaskuominaisuudet kuin reaaliluvuilla olisivat voimassa myös tässä kuvitellussa laajemmassa joukossa. Silloin siinä joukossa olisi oltava myös mm. kaikki muotoa 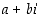 olevat luvut, joissa
olevat luvut, joissa 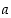 ja
ja 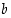 ovat mitä tahansa reaalilukuja. Edelleen kaikki näiden summat, erotukset, tulot ja osamäärät. Muodostetaan kahden tällaisen luvun
ovat mitä tahansa reaalilukuja. Edelleen kaikki näiden summat, erotukset, tulot ja osamäärät. Muodostetaan kahden tällaisen luvun 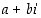 ja
ja 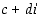 summa ja tulo. Oletamme siis, että "luvulla"
summa ja tulo. Oletamme siis, että "luvulla" 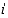 voidaan laskea kuin reaalilukumuuttujalla yleensäkin. Silloin summalle saadaan
voidaan laskea kuin reaalilukumuuttujalla yleensäkin. Silloin summalle saadaan 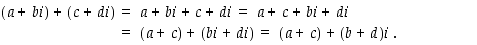
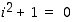 eli
eli 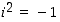 ,
saadaan tulolle vastaavasti
,
saadaan tulolle vastaavasti 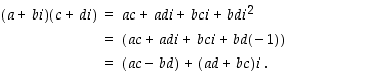
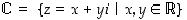 ,
,
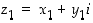 ja
ja 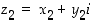 yhteen- ja kertolasku määritellään säännöillä
yhteen- ja kertolasku määritellään säännöillä 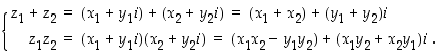
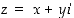 on
on 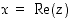 sen reaaliosa
sen reaaliosa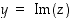 sen imaginaariosa
sen imaginaariosa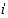 sanotaan imaginaariyksiköksi
sanotaan imaginaariyksiköksi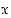 on siis myös kompleksiluku:
on siis myös kompleksiluku: 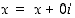 . Kompleksiluku on taas aito
. Kompleksiluku on taas aito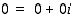 .
. 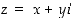 vastaluku
vastaluku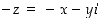 ,
ja
,
ja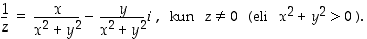
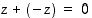 ja (b)
ja (b) 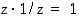 . Näistä kohta (a) on ilmeinen ja kohta (b) jätetään harjoitustehtäväksi (tehtävä
. Näistä kohta (a) on ilmeinen ja kohta (b) jätetään harjoitustehtäväksi (tehtävä 
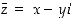 sanotaan luvun
sanotaan luvun 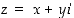 liittoluvuksi
liittoluvuksi 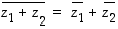 ja
ja 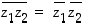 ,
,
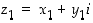 ja
ja 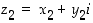 . Näiden sääntöjen todennus jätetään harjoitustehtäväksi (tehtävä
. Näiden sääntöjen todennus jätetään harjoitustehtäväksi (tehtävä