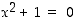Algebran peruslause

Reaaliluvut laajennettiin kompleksiluvuiksi sen takia, että yhtälölle 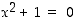saataisiin ratkaisu. Tästä on seurauksena kuitenkin se hämmästyttävä tosiasia, että samantien kaikille muillekin polynomeille löytyy ratkaisu.

Lause 1.7.7. (Algebran peruslause)

Jokaisella positiiviasteisella kompleksilukukertoimisella polynomilla on ainakin yksi (reaalinen tai kompleksinen) juuri. Jos moninkertaiset juuret lasketaan mukaan niin monta kertaa kuin niiden kertaluku osoittaa, on positiiviasteisella kompleksilukukertoimisella polynomilla yhtä monta juurta kuin sen aste on. Jokainen kompleksilukukertoiminen polynomi voidaan edelleen esittää muodossa

,

missä 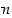on polynomin aste, 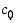on jokin kompleksiluku ja kompleksiluvut 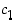, , 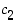..., 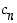ovat polynomin juuria.

Algebran peruslauseen todistus on täysin tämän esityksen ulottumattomissa ja jätetään matematiikassa syventäviä opintoja tai jatko-opintoja tekeville.

Reaalilukukertoimisella toisen asteen polynomilla 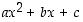on kompleksiset juuret, jos sen diskriminantti 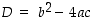on negatiivinen, ja sen juuret

ovat silloin toistensa liittolukuja.

Yleisesti voi osoittaa, että jos reaalilukukertoimisella polynomilla on kompleksinen juuri 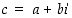, niin myös liittoluku 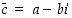on sen juuri (ks. harjoitustehtävä 55). Silloin tällaisella polynomilla on tekijänä tulo

,

joka on reaalikertoiminen polynomi. Tämä antaa todistusidean seuraavaan tulokseen. Yksityiskohtainen todistus kuitenkin sivuutetaan.

Lause 1.7.8.

Jokainen positiiviasteinen reaalilukukertoiminen polynomi voidaan esittää ensimmäisen ja toisen asteen reaalilukukertoimisten polynomien tulona.

Esimerkki 1.7.9.

Polynomille 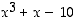on helppo keksiä yhdeksi juureksi 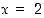. Siten se on jaollinen polynomilla 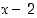. Jakolaskun jälkeen (esimerkiksi jakokulmalla) saadaan, että

.

Saadun toisen asteen tekijäpolynomin diskriminantti on 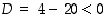, joten sillä ei ole reaalisia juuria. Siten edellä oleva esitys on tarkastellun polynomin reaalinen tekijöihinjako.

Polynomilla 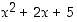on kuitenkin kompleksiset juuret 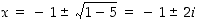. Siten tarkastellun polynomin kompleksinen tekijöihinjako on

.