Bijektio ja käänteiskuvaus
Jatketaan kuvausten perusasioitten kertaamista tarkastelemalla sellaisia kuvauksia, jotka kuvaavat kaikki alkiot eri alkioiksi.
• Funktio 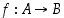 on injektio, jos se kuvaa kaikki alkiot eri alkioiksi ts. jos
on injektio, jos se kuvaa kaikki alkiot eri alkioiksi ts. jos 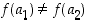 aina, kun
aina, kun 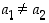 . On sama asia vaatia, että ehdosta
. On sama asia vaatia, että ehdosta 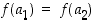 seuraa aina, että
seuraa aina, että 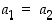 . Tätä muotoa on usein edullista käyttää silloin, kun funktio on määritelty lausekkeella. Kuvan 5 funktio ei ole injektio, sillä
. Tätä muotoa on usein edullista käyttää silloin, kun funktio on määritelty lausekkeella. Kuvan 5 funktio ei ole injektio, sillä 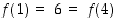 . Sen sijaan kuvan 6 mukainen funktio f' on injektio.
. Sen sijaan kuvan 6 mukainen funktio f' on injektio.
Kuva 6.
• Funktio 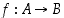 on surjektio (eli epijektio), jos sen kuvajoukko on koko maalijoukko ts. jos jokaiselle
on surjektio (eli epijektio), jos sen kuvajoukko on koko maalijoukko ts. jos jokaiselle 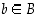 löytyy sellainen
löytyy sellainen 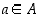 ,
että
,
että 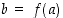 . Kuvien 5 ja 6 funktiot eivät ole surjektioita, sillä edellisessä alkiolla 7 ja jälkimmäisessä alkiolla 6 ei ole alkukuvaa. Sen sijaan kuvan 7 funktio f'' on surjektio (mutta ei vuorostaan ole injektio).
. Kuvien 5 ja 6 funktiot eivät ole surjektioita, sillä edellisessä alkiolla 7 ja jälkimmäisessä alkiolla 6 ei ole alkukuvaa. Sen sijaan kuvan 7 funktio f'' on surjektio (mutta ei vuorostaan ole injektio).
Kuva 7.
• Funktio 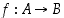 on bijektio, jos se on sekä injektio että surjektio eli jos jokaista
on bijektio, jos se on sekä injektio että surjektio eli jos jokaista 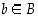 vastaa täsmälleen yksi
vastaa täsmälleen yksi 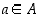 ,
jolle
,
jolle 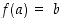 . Edellä olevien kuvien 5, 6 ja 7 funktioista mikään ei ole bijektio, sillä näistä ensimmäinen ei ole injektio eikä surjektio, toinen ei ole surjektio ja kolmas ei ole injektio. Kuvan 8 funktiot
. Edellä olevien kuvien 5, 6 ja 7 funktioista mikään ei ole bijektio, sillä näistä ensimmäinen ei ole injektio eikä surjektio, toinen ei ole surjektio ja kolmas ei ole injektio. Kuvan 8 funktiot 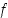 ja
ja 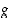 sen sijaan ovat bijektioita.
sen sijaan ovat bijektioita.
Opiskeluvideo: F5: Funktiot 5 − surjektio ja bijektio 

• Identtinen kuvaus on kuvaus 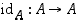 ,
jolle
,
jolle 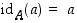 kaikilla
kaikilla 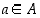 .
.
• Kahden funktion 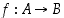 ja
ja 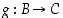 yhdistetty kuvaus on se kuvaus
yhdistetty kuvaus on se kuvaus 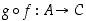 ,
jolle
,
jolle 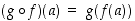 kaikille
kaikille 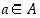 (merkintä
(merkintä 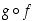 luetaan "
luetaan "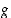 pallo
pallo 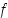 "). Yhdistetyssä kuvauksessa ensin muuttujaan
"). Yhdistetyssä kuvauksessa ensin muuttujaan 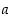 sovellettava funktio
sovellettava funktio 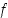 on sisäfunktio ja sen jälkeen saatuun tulokseen
on sisäfunktio ja sen jälkeen saatuun tulokseen 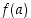 sovellettava funktio
sovellettava funktio 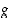 on ulkofunktio. Yhdistetyn funktion määrittelyssä ei välttämättä funktion
on ulkofunktio. Yhdistetyn funktion määrittelyssä ei välttämättä funktion 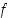 maalijoukon ja funktion
maalijoukon ja funktion 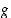 määrittelyjoukon tarvitse olla sama joukko, vaan yleisemmin määriteltynä riittää, että ulkofunktio
määrittelyjoukon tarvitse olla sama joukko, vaan yleisemmin määriteltynä riittää, että ulkofunktio 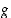 on määritelty sisäfunktion
on määritelty sisäfunktion 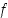 kuvapisteissä, ts. on riittävää, että
kuvapisteissä, ts. on riittävää, että 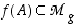 .
.
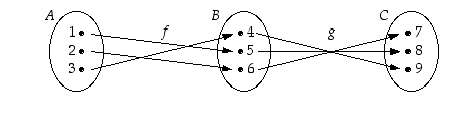
Esimerkkinä kuvassa 8 on esitetty kaksi funktiota 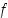 ja
ja 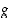 ,
joille voidaan muodostaa yhdistetty funktio
,
joille voidaan muodostaa yhdistetty funktio 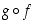 .
.
Kuva 8.
Tälle yhdistetylle funktiolle on esimerkiksi 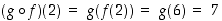 . Tuloksena oleva yhdistetty kuvaus
. Tuloksena oleva yhdistetty kuvaus 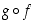 on esitetty kuvassa 9.
on esitetty kuvassa 9.
Kuva 9.
Opiskeluvideo: F6: Funktiot 6 − yhdistetty funktio 

• Bijektion 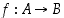 käänteiskuvaus on se kuvaus
käänteiskuvaus on se kuvaus 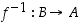 ,
jolle
,
jolle 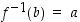 täsmälleen silloin, kun
täsmälleen silloin, kun 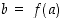 . Sama voidaan ilmaista vaatimalla, että
. Sama voidaan ilmaista vaatimalla, että 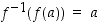 kaikilla
kaikilla 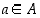 ja
ja 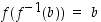 kaikilla
kaikilla 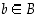 . Nämä ehdot voidaan ilmoittaa myös ilman muuttujia muodossa
. Nämä ehdot voidaan ilmoittaa myös ilman muuttujia muodossa 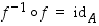 ja
ja 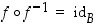 .
.
Kuvan 8 funktiot 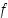 ja
ja 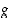 ovat molemmat bijektioita ja niillä on kummallakin siten käänteisfunktio. Esimerkiksi funktion
ovat molemmat bijektioita ja niillä on kummallakin siten käänteisfunktio. Esimerkiksi funktion 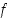 käänteisfunktiolle on
käänteisfunktiolle on 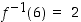 ja funktion
ja funktion 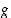 käänteisfunktiolle on
käänteisfunktiolle on 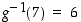 .
.
Havainnollistus: Käänteisfunktion muodostaminen 1 
Havainnollistus: Käänteisfunktion muodostaminen 2 
Havainnollistus: Käänteisfunktion muodostaminen 3 
Opiskeluvideo: F7: Funktiot 7 − käänteisfunktio 

• Kahden bijektion 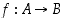 ja
ja 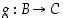 yhdistetty kuvaus
yhdistetty kuvaus 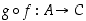 on myös bijektio, ja sillä on siten käänteisfunktio. Lisäksi tälle pätee sääntö
on myös bijektio, ja sillä on siten käänteisfunktio. Lisäksi tälle pätee sääntö 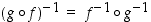 .
.
Kuvan 8 funktiot 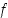 ja
ja 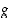 ovat bijektioita ja siten myös niiden yhdistetty kuvaus, joka on esitetty kuvassa 9. Tälle esimerkiksi
ovat bijektioita ja siten myös niiden yhdistetty kuvaus, joka on esitetty kuvassa 9. Tälle esimerkiksi 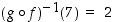 ,
mikä saadaan myös seuraavasti:
,
mikä saadaan myös seuraavasti:
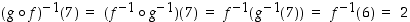 .
.
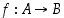 on injektio, jos se kuvaa kaikki alkiot eri alkioiksi ts. jos
on injektio, jos se kuvaa kaikki alkiot eri alkioiksi ts. jos 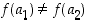 aina, kun
aina, kun 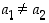 . On sama asia vaatia, että ehdosta
. On sama asia vaatia, että ehdosta 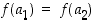 seuraa aina, että
seuraa aina, että 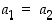 . Tätä muotoa on usein edullista käyttää silloin, kun funktio on määritelty lausekkeella. Kuvan 5 funktio ei ole injektio, sillä
. Tätä muotoa on usein edullista käyttää silloin, kun funktio on määritelty lausekkeella. Kuvan 5 funktio ei ole injektio, sillä 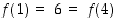 . Sen sijaan kuvan 6 mukainen funktio f' on injektio.
. Sen sijaan kuvan 6 mukainen funktio f' on injektio. 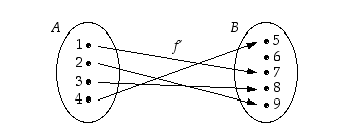
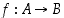 on surjektio
on surjektio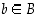 löytyy sellainen
löytyy sellainen 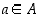 ,
että
,
että 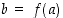 . Kuvien
. Kuvien 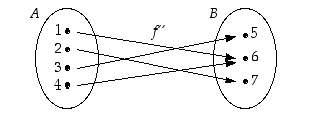
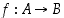 on bijektio
on bijektio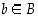 vastaa täsmälleen yksi
vastaa täsmälleen yksi 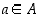 ,
jolle
,
jolle 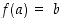 . Edellä olevien kuvien
. Edellä olevien kuvien 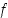 ja
ja 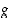 sen sijaan ovat bijektioita.
sen sijaan ovat bijektioita. 

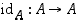 ,
jolle
,
jolle 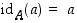 kaikilla
kaikilla 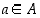 .
. 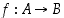 ja
ja 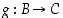 yhdistetty
yhdistetty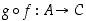 ,
jolle
,
jolle 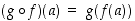 kaikille
kaikille 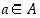 (merkintä
(merkintä 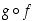 luetaan "
luetaan "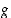 pallo
pallo 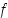 "). Yhdistetyssä kuvauksessa ensin muuttujaan
"). Yhdistetyssä kuvauksessa ensin muuttujaan 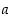 sovellettava funktio
sovellettava funktio 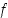 on sisäfunktio
on sisäfunktio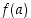 sovellettava funktio
sovellettava funktio 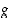 on ulkofunktio
on ulkofunktio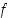 maalijoukon ja funktion
maalijoukon ja funktion 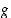 määrittelyjoukon tarvitse olla sama joukko, vaan yleisemmin määriteltynä riittää, että ulkofunktio
määrittelyjoukon tarvitse olla sama joukko, vaan yleisemmin määriteltynä riittää, että ulkofunktio 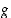 on määritelty sisäfunktion
on määritelty sisäfunktion 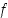 kuvapisteissä, ts. on riittävää, että
kuvapisteissä, ts. on riittävää, että 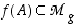 .
. 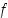 ja
ja 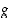 ,
joille voidaan muodostaa yhdistetty funktio
,
joille voidaan muodostaa yhdistetty funktio 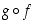 .
.
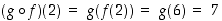 . Tuloksena oleva yhdistetty kuvaus
. Tuloksena oleva yhdistetty kuvaus 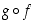 on esitetty kuvassa
on esitetty kuvassa 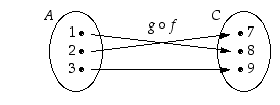


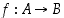 käänteiskuvaus
käänteiskuvaus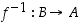 ,
jolle
,
jolle 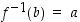 täsmälleen silloin, kun
täsmälleen silloin, kun 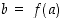 . Sama voidaan ilmaista vaatimalla, että
. Sama voidaan ilmaista vaatimalla, että 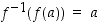 kaikilla
kaikilla 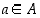 ja
ja 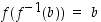 kaikilla
kaikilla 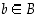 . Nämä ehdot voidaan ilmoittaa myös ilman muuttujia muodossa
. Nämä ehdot voidaan ilmoittaa myös ilman muuttujia muodossa 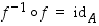 ja
ja 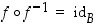 .
. 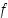 ja
ja 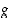 ovat molemmat bijektioita ja niillä on kummallakin siten käänteisfunktio. Esimerkiksi funktion
ovat molemmat bijektioita ja niillä on kummallakin siten käänteisfunktio. Esimerkiksi funktion 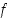 käänteisfunktiolle on
käänteisfunktiolle on 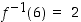 ja funktion
ja funktion 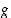 käänteisfunktiolle on
käänteisfunktiolle on 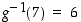 .
. 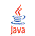
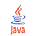
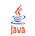


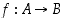 ja
ja 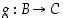 yhdistetty kuvaus
yhdistetty kuvaus 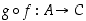 on myös bijektio, ja sillä on siten käänteisfunktio. Lisäksi tälle pätee sääntö
on myös bijektio, ja sillä on siten käänteisfunktio. Lisäksi tälle pätee sääntö 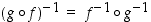 .
. 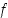 ja
ja 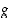 ovat bijektioita ja siten myös niiden yhdistetty kuvaus, joka on esitetty kuvassa
ovat bijektioita ja siten myös niiden yhdistetty kuvaus, joka on esitetty kuvassa 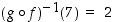 ,
mikä saadaan myös seuraavasti:
,
mikä saadaan myös seuraavasti: 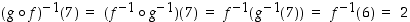 .
.