Funktion määrittely sekä joukon kuva ja alkukuva
Matematiikassa tarkastellaan usein muuttujien välisiä riippuvuuksia. Esimerkiksi neliön pinta-ala riippuu sen sivun pituudesta ja ympyrän kehän pituus ja pinta-ala riippuvat sen säteestä. Tällainen riippuvuus voidaan ilmaista kuvauksena, jossa tulos (pinta-ala, pituus, ...) ilmoitetaan riippuvuutena syötteestä (pituus, säde, ...). Esitetään seuraavassa kertauksen- ja luettelonomaisesti muutamia perusasioita kuvauksista.
• Funktio eli kuvaus 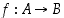 on sääntö (relaatio), joka liittää kuhunkin lähtöjoukon eli määrittelyjoukon
on sääntö (relaatio), joka liittää kuhunkin lähtöjoukon eli määrittelyjoukon 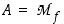 alkioon
alkioon 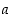 yhden (ja vain yhden) maalijoukon
yhden (ja vain yhden) maalijoukon 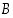 alkion
alkion 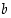 . Tätä yhteyttä merkitään
. Tätä yhteyttä merkitään 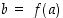 ja alkiota
ja alkiota 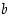 sanotaan alkion
sanotaan alkion 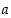 kuvaksi tai funktion
kuvaksi tai funktion 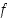 arvoksi pisteessä
arvoksi pisteessä 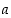 .
.
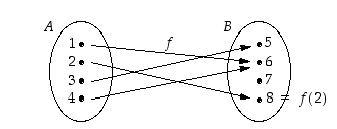
Esimerkkinä alla olevassa kuvassa 5 on esitettynä kuvaus 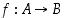 ,
missä lähtöjoukkona on joukko
,
missä lähtöjoukkona on joukko 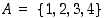 ja maalijoukkona joukko
ja maalijoukkona joukko 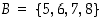 . Tässä kuvauksessa on esimerkiksi
. Tässä kuvauksessa on esimerkiksi 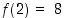 .
.
Kuva 5.
• Kuvauksessa 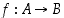 osajoukon
osajoukon 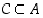 kuva(joukko) on kaikkien joukon
kuva(joukko) on kaikkien joukon 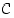 alkioiden kuvien muodostama joukko
alkioiden kuvien muodostama joukko
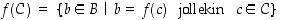 .
.
Yllä olevassa kuvan 5 esimerkissä joukon 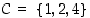 kuva on joukko
kuva on joukko 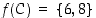 .
.
• Edellisestä erikoistapauksena funktion 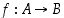 kuvajoukko eli arvojoukko on koko joukon
kuvajoukko eli arvojoukko on koko joukon 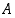 kuvajoukko
kuvajoukko
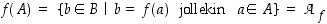 .
.
Kuvan 5 esimerkissä arvojoukko on 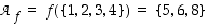 .
.
• Osajoukon 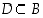 alkukuva on joukon
alkukuva on joukon 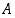 osajoukko
osajoukko
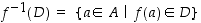 .
.
Joukon 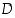 alkukuvasta käytetään myös merkintää
alkukuvasta käytetään myös merkintää 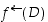 ,
jotta tämä erottuisi myöhemmin esitettävästä käänteiskuvauksen kuvasta (ks. Bijektio ja käänteiskuvaus). Kuvan 5 esimerkissä joukon
,
jotta tämä erottuisi myöhemmin esitettävästä käänteiskuvauksen kuvasta (ks. Bijektio ja käänteiskuvaus). Kuvan 5 esimerkissä joukon 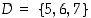 alkukuva on joukko
alkukuva on joukko 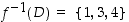 .
.
• Edellisestä erikoistapauksena alkion 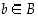 alkukuva on joukko
alkukuva on joukko
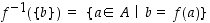 .
.
Alkion 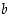 alkukuvasta käytetään myös merkintää
alkukuvasta käytetään myös merkintää 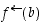 . Kuvan 5 esimerkissä alkion
. Kuvan 5 esimerkissä alkion 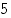 alkukuva on joukko
alkukuva on joukko 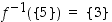 ja alkion
ja alkion 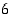 alkukuva on joukko
alkukuva on joukko 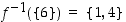 .
.
Opiskeluvideo: F1: Funktiot 1 − määritelmä 

Opiskeluvideo: F2: Funktiot 2 − kuvajoukko 

Opiskeluvideo: F3: Funktiot 3 − alkukuva 

Opiskeluvideo: F4: Funktiot 4 − injektio 

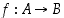 on sääntö (relaatio), joka liittää kuhunkin lähtöjoukon eli määrittelyjoukon
on sääntö (relaatio), joka liittää kuhunkin lähtöjoukon eli määrittelyjoukon 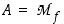 alkioon
alkioon 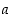 yhden (ja vain yhden) maalijoukon
yhden (ja vain yhden) maalijoukon 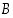 alkion
alkion 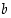 . Tätä yhteyttä merkitään
. Tätä yhteyttä merkitään 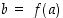 ja alkiota
ja alkiota 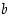 sanotaan alkion
sanotaan alkion 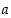 kuvaksi tai funktion
kuvaksi tai funktion 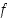 arvoksi pisteessä
arvoksi pisteessä 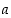 .
. 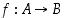 ,
missä lähtöjoukkona on joukko
,
missä lähtöjoukkona on joukko 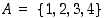 ja maalijoukkona joukko
ja maalijoukkona joukko 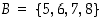 . Tässä kuvauksessa on esimerkiksi
. Tässä kuvauksessa on esimerkiksi 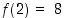 .
. 
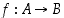 osajoukon
osajoukon 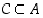 kuva
kuva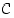 alkioiden kuvien muodostama joukko
alkioiden kuvien muodostama joukko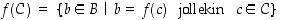 .
. 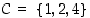 kuva on joukko
kuva on joukko 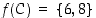 .
. 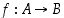 kuvajoukko
kuvajoukko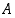 kuvajoukko
kuvajoukko 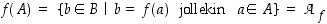 .
. 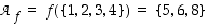 .
. 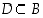 alkukuva
alkukuva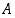 osajoukko
osajoukko 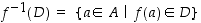 .
. 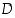 alkukuvasta käytetään myös merkintää
alkukuvasta käytetään myös merkintää 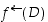 ,
jotta tämä erottuisi myöhemmin esitettävästä käänteiskuvauksen kuvasta (ks.
,
jotta tämä erottuisi myöhemmin esitettävästä käänteiskuvauksen kuvasta (ks. 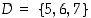 alkukuva on joukko
alkukuva on joukko 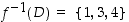 .
. 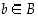 alkukuva
alkukuva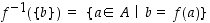 .
. 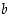 alkukuvasta käytetään myös merkintää
alkukuvasta käytetään myös merkintää 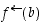 . Kuvan
. Kuvan 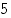 alkukuva on joukko
alkukuva on joukko 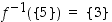 ja alkion
ja alkion 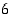 alkukuva on joukko
alkukuva on joukko 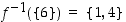 .
. 






