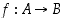 ,
missä sekä lähtöjoukko
,
missä sekä lähtöjoukko 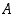 että maalijoukko
että maalijoukko 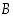 ovat reaalilukujoukkoja. Yleensä maalijoukkona on koko reaalilukujen joukko eli
ovat reaalilukujoukkoja. Yleensä maalijoukkona on koko reaalilukujen joukko eli 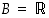 ja usein myös määrittelyjoukkona on koko reaalilukujen joukko eli
ja usein myös määrittelyjoukkona on koko reaalilukujen joukko eli 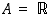 .
.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Reaalifunktioiksi sanotaan kaikkia sellaisia kuvauksia 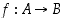 ,
missä sekä lähtöjoukko
,
missä sekä lähtöjoukko 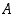 että maalijoukko
että maalijoukko 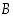 ovat reaalilukujoukkoja. Yleensä maalijoukkona on koko reaalilukujen joukko eli
ovat reaalilukujoukkoja. Yleensä maalijoukkona on koko reaalilukujen joukko eli 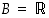 ja usein myös määrittelyjoukkona on koko reaalilukujen joukko eli
ja usein myös määrittelyjoukkona on koko reaalilukujen joukko eli 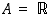 .
.
Funktio 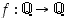 ,
jolle
,
jolle 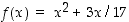 ,
on reaalifunktio, jonka määrittely on rajattu rationaaliluvuille. Huomaa, että funktion lausekkeen antamat tulokset ovat rationaalilukuja, joten maalijoukkona voi olla rationaalilukujen joukko
,
on reaalifunktio, jonka määrittely on rajattu rationaaliluvuille. Huomaa, että funktion lausekkeen antamat tulokset ovat rationaalilukuja, joten maalijoukkona voi olla rationaalilukujen joukko 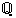 .
.
Edellä olevan lausekkeen 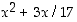 arvo voidaan muodostaa myös kaikille reaaliluvuille, mutta silloin määrittelyjoukon lisäksi maalijoukkoakin on laajennettava, ilmeisestikin välttämättä koko reaalilukujen joukoksi. Saatu funktio
arvo voidaan muodostaa myös kaikille reaaliluvuille, mutta silloin määrittelyjoukon lisäksi maalijoukkoakin on laajennettava, ilmeisestikin välttämättä koko reaalilukujen joukoksi. Saatu funktio 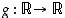 ,
jolle
,
jolle 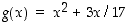 ,
on periaatteessa eri funktio kuin
,
on periaatteessa eri funktio kuin 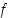 .
.
Reaalifunktio ilmaistaan usein kuitenkin pelkällä lausekkeella ilmoittamatta ollenkaan sen lähtö- ja maalijoukkoja. Silloin määrittelyjoukoksi ajatellaan laajin reaalilukujoukko, jossa lausekkeen arvo voidaan muodostaa.
määrittelyssä oleva lauseke voidaan muodostaa kaikilla luvuilla 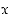 ,
joilla nimittäjä ei ole nolla. Tässä tapauksessa määrittelyjoukko on siis
,
joilla nimittäjä ei ole nolla. Tässä tapauksessa määrittelyjoukko on siis
Määritellään funktio 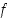 lausekkeella
lausekkeella 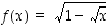 . Kyseessä on yhdistetty funktio
. Kyseessä on yhdistetty funktio 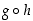 ,
missä sisäfunktio on
,
missä sisäfunktio on 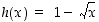 ja ulkofunktio on
ja ulkofunktio on 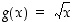 . Kumpikin on määritelty silloin, kun
. Kumpikin on määritelty silloin, kun 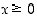 .
.
Yhdistetty funktio 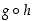 on siten määritelty niissä pisteissä
on siten määritelty niissä pisteissä 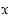 ,
joissa funktio
,
joissa funktio 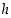 on määritelty ja joille
on määritelty ja joille 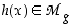 . Näin ollen se on määritelty, kun
. Näin ollen se on määritelty, kun 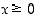 ja
ja 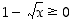 . Jälkimmäinen ehto on yhtäpitävää ehdon
. Jälkimmäinen ehto on yhtäpitävää ehdon 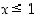 kanssa (kun lisäksi
kanssa (kun lisäksi 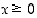 ). Siten
). Siten 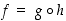 on määritelty, kun
on määritelty, kun 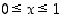 ,
eli
,
eli 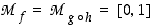 .
.
Reaalifunktiolle 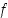 luku (piste)
luku (piste) 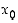 on sen nollakohta tai juuri, jos
on sen nollakohta tai juuri, jos 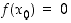 . Edellä olevan esimerkin 1.5.3 funktiolla
. Edellä olevan esimerkin 1.5.3 funktiolla
on ainakin yksi (osoittajan) nollakohta, piste 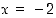 . Sen osoittamiseen, että muita nollakohtia ei ole, tarvitaan myöhemmin käsiteltäviä menetelmiä (mm. funktion monotonisuuden selvittämistä).
. Sen osoittamiseen, että muita nollakohtia ei ole, tarvitaan myöhemmin käsiteltäviä menetelmiä (mm. funktion monotonisuuden selvittämistä).