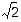Algebrallinen luku

Edellä olevan esimerkin 1.3.1 mukaan rationaalilukuihin voidaan lisätä neliöjuuri 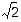ja tutkia, millä lukujoukolla on, kuten rationaaliluvuilla, se ominaisuus, että sen alkioiden summat, erotukset, tulot ja osamäärät ovat edelleen sen lukuja. Osoittautuu, että pienimmäksi tällaiseksi lukualueeksi kelpaa joukko

.

Seuraava esimerkki havainnollistaa (mutta ei todista) sitä, että näiden neljän peruslaskutoimituksen tulokset pysyvät tässä joukossa.

Esimerkki 1.3.2.

Luvuille ja on

,

,

ja

Osamäärän muokkauksessa on neliöjuuren poistamiseksi nimittäjästä lavennettu osamäärä nimittäjän summaa vastaavalla erotuksella ja käytetty sitten hyväksi tulosääntöä 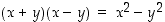. Tuloksista havaitaan, että kaikki saadut lausekkeet ovat muoto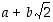a , miss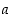ä ja 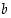ovat rationaalilukuja. Konkreettien lukujen sijasta yllä olevat laskut voidaan toistaa yleisesti muotoa 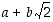oleville luvuille (ks. harjoitustehtävä 8).

Lukujoukkoon 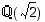voidaan edelleen lisätä muita neliöjuuria, korkeampiasteisia juuria tai vielä yleisemmin rationaalilukukertoimisten polynomien juuria. Tällä tavalla ei kuitenkaan saada vielä kaikkia reaalilukuja vaan vasta ns. algebralliset luvut.

Algebralliset luvut ovat sellaisia reaalilukuja, jotka ovat jonkin rationaalilukukertoimisen (ja samalla itse asiassa myös kokonaislukukertoimisen) polynomin juuria. Itse rationaalilukujen lisäksi tällaisia ovat esimerkiksi 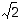, 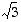ja 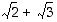− nämä ovat nimittäin vastaavasti polynomien 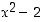, 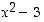ja 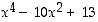juuria.

Muut reaaliluvut kuin algebralliset luvut ovat transkendenttisia lukuja. Tällainen on esimerkiksi ympyrän kaaren ja halkaisijan pituuksien suhde 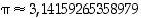samoin kuin eksponenttifunktion ja luonnollisen logaritmifunktion kantaluku, ns. Neperin luku 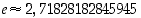(ks. pykälä Neperin luku e). Edellisen luvun transkendenttisuuden todisti C.L.F. Lindemann v. 1882 ja jälkimmäisen Charles Hermite v. 1873. Vuonna 1923 A. Gelfond osoitti, että myös luku 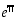on transkendenttinen. Toistaiseksi ei tiedetä, ovatko myös luvut 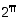, 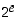ja 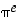transkendenttisia (tällaisten lukujen tarkka määrittely annetaan pykälässä Yleinen eksponenttifunktio ja logaritmifunktio).