Rationaaliluku
Erilaisten yhtälöiden ratkaisutarve on johtanut lukualueiden laajentamisiin. Esimerkiksi yhtälöllä 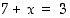 ei ole ratkaisua luonnollisten lukujen
ei ole ratkaisua luonnollisten lukujen 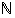 joukossa. Tämä ongelma poistuu ottamalla käyttöön negatiiviset kokonaisluvut ja sitä myötä kaikkien kokonaislukujen joukko
joukossa. Tämä ongelma poistuu ottamalla käyttöön negatiiviset kokonaisluvut ja sitä myötä kaikkien kokonaislukujen joukko 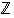 . Tämän jälkeen ratkeavat kaikki muotoa
. Tämän jälkeen ratkeavat kaikki muotoa 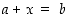 yhtälöt, missä
yhtälöt, missä 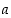 ja
ja 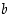 ovat mitä tahansa luonnollisia lukuja. Vastaavasti yhtälö
ovat mitä tahansa luonnollisia lukuja. Vastaavasti yhtälö 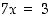 ja yleisesti kaikki kokonaislukuyhtälöt
ja yleisesti kaikki kokonaislukuyhtälöt 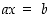 (
(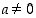 ) ratkeavat rationaalilukujen eli murtolukujen joukossa
) ratkeavat rationaalilukujen eli murtolukujen joukossa
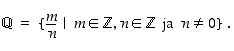
Rationaaliluvut 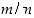 ja
ja 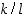 (missä
(missä 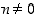 ja
ja 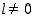 ) ovat samat, jos
) ovat samat, jos 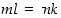 . Rationaaliluvuilla on sellainen tärkeä ominaisuus, että sen alkioiden summat, erotukset, tulot ja osamäärät ovat edelleen rationaalilukuja. Tämän osoittavat laskusäännöt
. Rationaaliluvuilla on sellainen tärkeä ominaisuus, että sen alkioiden summat, erotukset, tulot ja osamäärät ovat edelleen rationaalilukuja. Tämän osoittavat laskusäännöt
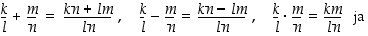
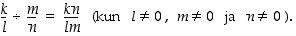
On kuitenkin yksinkertaisia yhtälöitä, jotka eivät ratkea rationaalilukujenkaan joukossa. Sellaisia ovat esimerkiksi 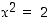 ja
ja 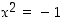 . Edellisen yhtälön kohdalta väite todennetaan seuraavassa esimerkissä ja jälkimmäistä yhtälöä tarkastellaan kompleksilukujen yhteydessä pykälässä Kompleksiluvuista.
. Edellisen yhtälön kohdalta väite todennetaan seuraavassa esimerkissä ja jälkimmäistä yhtälöä tarkastellaan kompleksilukujen yhteydessä pykälässä Kompleksiluvuista.
Esimerkki 1.3.1.
Osoitetaan, että yhtälöllä 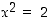 ei ole rationaalilukuratkaisua. Oletetaan päinvastoin kuin väitetään, että tällä yhtälöllä on rationaalinen ratkaisu
ei ole rationaalilukuratkaisua. Oletetaan päinvastoin kuin väitetään, että tällä yhtälöllä on rationaalinen ratkaisu 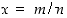 ,
missä voimme olettaa, että murtoluku on supistetussa muodossa eli osoittajalla
,
missä voimme olettaa, että murtoluku on supistetussa muodossa eli osoittajalla 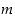 ja nimittäjällä
ja nimittäjällä 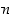 ei ole ykköstä isompaa kokonaislukua yhteisenä tekijänään. Käytämme jatkossa sitä tietoa, että parillisten kokonaislukujen neliöt ovat parillisia ja parittomien kokonaislukujen neliöt ovat vastaavasti parittomia. Jos nimittäin luku
ei ole ykköstä isompaa kokonaislukua yhteisenä tekijänään. Käytämme jatkossa sitä tietoa, että parillisten kokonaislukujen neliöt ovat parillisia ja parittomien kokonaislukujen neliöt ovat vastaavasti parittomia. Jos nimittäin luku 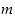 on parillinen, se on muotoa
on parillinen, se on muotoa 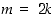 ,
jolloin yhtälöstä
,
jolloin yhtälöstä 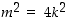 nähdään, että myös
nähdään, että myös 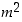 on parillinen luku. Jos taas luku
on parillinen luku. Jos taas luku 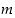 on pariton, se on muotoa
on pariton, se on muotoa 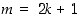 ,
jolloin yhtälöstä
,
jolloin yhtälöstä
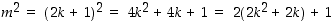
nähdään, että myös 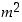 on pariton.
on pariton.
Vastaväitteen mukaisesti oletetaan, että luvulle 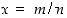 on
on 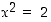 . Siten
. Siten 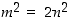 . Tämä osoittaa, että
. Tämä osoittaa, että 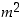 on parillinen luku. Silloin myös luvun
on parillinen luku. Silloin myös luvun 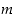 on oltava parillinen, sillä parittomien lukujen neliöt olisivat parittomia kuten edellä todettiin.
on oltava parillinen, sillä parittomien lukujen neliöt olisivat parittomia kuten edellä todettiin.
Luku 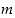 on parillisena muotoa
on parillisena muotoa 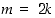 ,
jolloin yhtälöstä
,
jolloin yhtälöstä 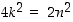 nähdään, että myös luku
nähdään, että myös luku 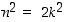 on parillinen. Siten edellä olevan mukaan myös
on parillinen. Siten edellä olevan mukaan myös 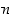 on parillinen.
on parillinen.
Mutta nyt sekä 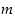 että
että 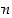 olisivat parillisia ja murtoluku
olisivat parillisia ja murtoluku 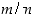 voitaisiin supistaa kakkosella, mikä on vastoin lähtötilannetta. Yhtälöllä
voitaisiin supistaa kakkosella, mikä on vastoin lähtötilannetta. Yhtälöllä 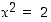 ei näin ollen voi olla rationaalilukuratkaisua.
ei näin ollen voi olla rationaalilukuratkaisua.

Edellä oleva esimerkki antaa hyvän mallin ns. antiteesi- eli vastaväitetodistukselle. Siinä todistettavalle väitteelle päinvastaisesti oletetaan antiteesinä, että sen vastaväite on voimassa, ja yritetään sen jälkeen osoittaa ristiriita oletuksen tai jonkun muun tiedetyn tosiasian kanssa. Esimerkissä 1.3.1 väitteelle, että yhtälöllä 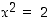 ei ole rationaalilukuratkaisua, muodostettiin vastaväite, jonka mukaan tällainen ratkaisu olisikin olemassa. Tehtyjen päättelyjen jälkeen todettiin ristiriitana, että tällainen ratkaisu ei voisi olla supistettua muotoa vaikka näin oletettaisiin. Loppupäätelmänä on, että antiteesi eli vastaväite ei voi pitää paikkansa vaan alkuperäinen väite on voimassa.
ei ole rationaalilukuratkaisua, muodostettiin vastaväite, jonka mukaan tällainen ratkaisu olisikin olemassa. Tehtyjen päättelyjen jälkeen todettiin ristiriitana, että tällainen ratkaisu ei voisi olla supistettua muotoa vaikka näin oletettaisiin. Loppupäätelmänä on, että antiteesi eli vastaväite ei voi pitää paikkansa vaan alkuperäinen väite on voimassa.
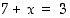 ei ole ratkaisua luonnollisten lukujen
ei ole ratkaisua luonnollisten lukujen 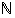 joukossa. Tämä ongelma poistuu ottamalla käyttöön negatiiviset kokonaisluvut ja sitä myötä kaikkien kokonaislukujen joukko
joukossa. Tämä ongelma poistuu ottamalla käyttöön negatiiviset kokonaisluvut ja sitä myötä kaikkien kokonaislukujen joukko 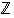 . Tämän jälkeen ratkeavat kaikki muotoa
. Tämän jälkeen ratkeavat kaikki muotoa 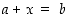 yhtälöt, missä
yhtälöt, missä 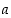 ja
ja 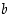 ovat mitä tahansa luonnollisia lukuja. Vastaavasti yhtälö
ovat mitä tahansa luonnollisia lukuja. Vastaavasti yhtälö 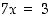 ja yleisesti kaikki kokonaislukuyhtälöt
ja yleisesti kaikki kokonaislukuyhtälöt 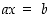 (
(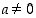 ) ratkeavat rationaalilukujen eli murtolukujen joukossa
) ratkeavat rationaalilukujen eli murtolukujen joukossa 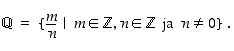
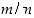 ja
ja 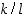 (missä
(missä 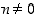 ja
ja 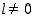 ) ovat samat, jos
) ovat samat, jos 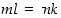 .
. 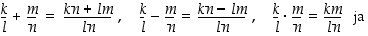
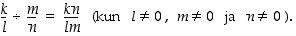
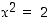 ja
ja 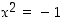 . Edellisen yhtälön kohdalta väite todennetaan seuraavassa esimerkissä ja jälkimmäistä yhtälöä tarkastellaan kompleksilukujen yhteydessä pykälässä
. Edellisen yhtälön kohdalta väite todennetaan seuraavassa esimerkissä ja jälkimmäistä yhtälöä tarkastellaan kompleksilukujen yhteydessä pykälässä 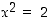 ei ole rationaalilukuratkaisua. Oletetaan päinvastoin kuin väitetään, että tällä yhtälöllä on rationaalinen ratkaisu
ei ole rationaalilukuratkaisua. Oletetaan päinvastoin kuin väitetään, että tällä yhtälöllä on rationaalinen ratkaisu 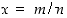 ,
missä voimme olettaa, että murtoluku on supistetussa muodossa eli osoittajalla
,
missä voimme olettaa, että murtoluku on supistetussa muodossa eli osoittajalla 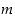 ja nimittäjällä
ja nimittäjällä 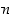 ei ole ykköstä isompaa kokonaislukua yhteisenä tekijänään. Käytämme jatkossa sitä tietoa, että parillisten kokonaislukujen neliöt ovat parillisia ja parittomien kokonaislukujen neliöt ovat vastaavasti parittomia. Jos nimittäin luku
ei ole ykköstä isompaa kokonaislukua yhteisenä tekijänään. Käytämme jatkossa sitä tietoa, että parillisten kokonaislukujen neliöt ovat parillisia ja parittomien kokonaislukujen neliöt ovat vastaavasti parittomia. Jos nimittäin luku 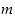 on parillinen, se on muotoa
on parillinen, se on muotoa 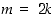 ,
jolloin yhtälöstä
,
jolloin yhtälöstä 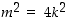 nähdään, että myös
nähdään, että myös 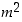 on parillinen luku. Jos taas luku
on parillinen luku. Jos taas luku 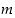 on pariton, se on muotoa
on pariton, se on muotoa 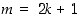 ,
jolloin yhtälöstä
,
jolloin yhtälöstä 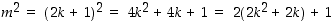
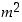 on pariton.
on pariton. 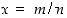 on
on 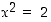 . Siten
. Siten 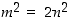 . Tämä osoittaa, että
. Tämä osoittaa, että 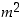 on parillinen luku. Silloin myös luvun
on parillinen luku. Silloin myös luvun 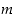 on oltava parillinen, sillä parittomien lukujen neliöt olisivat parittomia kuten edellä todettiin.
on oltava parillinen, sillä parittomien lukujen neliöt olisivat parittomia kuten edellä todettiin. 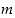 on parillisena muotoa
on parillisena muotoa 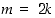 ,
jolloin yhtälöstä
,
jolloin yhtälöstä 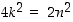 nähdään, että myös luku
nähdään, että myös luku 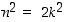 on parillinen. Siten edellä olevan mukaan myös
on parillinen. Siten edellä olevan mukaan myös 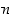 on parillinen.
on parillinen. 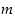 että
että 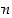 olisivat parillisia ja murtoluku
olisivat parillisia ja murtoluku 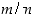 voitaisiin supistaa kakkosella, mikä on vastoin lähtötilannetta. Yhtälöllä
voitaisiin supistaa kakkosella, mikä on vastoin lähtötilannetta. Yhtälöllä 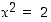 ei näin ollen voi olla rationaalilukuratkaisua.
ei näin ollen voi olla rationaalilukuratkaisua. 
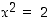 ei ole rationaalilukuratkaisua, muodostettiin vastaväite, jonka mukaan tällainen ratkaisu olisikin olemassa. Tehtyjen päättelyjen jälkeen todettiin ristiriitana, että tällainen ratkaisu ei voisi olla supistettua muotoa vaikka näin oletettaisiin. Loppupäätelmänä on, että antiteesi eli vastaväite ei voi pitää paikkansa vaan alkuperäinen väite on voimassa.
ei ole rationaalilukuratkaisua, muodostettiin vastaväite, jonka mukaan tällainen ratkaisu olisikin olemassa. Tehtyjen päättelyjen jälkeen todettiin ristiriitana, että tällainen ratkaisu ei voisi olla supistettua muotoa vaikka näin oletettaisiin. Loppupäätelmänä on, että antiteesi eli vastaväite ei voi pitää paikkansa vaan alkuperäinen väite on voimassa.