Neperin luku e

Tarkastellaan seuraavaa lukujonoa

Jonon alkupään termien (liki)arvoja ovat: , , , , , ..., , ..., .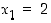

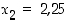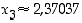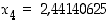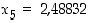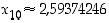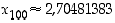Voidaan osoittaa, että yleisesti

ts. jono 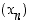on aidosti kasvava ja ylhäältä rajoitettu, joten sillä on raja-arvo (joka on korkeintaan 4). Tätä raja-arvoa sanotaan Neperin luvuksi 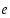, siis

Luku 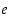on transkendenttinen luku, jonka likiarvo on .

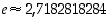Edellä olevalla lukujonolla 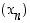on kumppanina jono 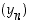, missä

Tästä lukujonosta voidaan osoittaa, että

,

ts. sekin on aidosti kasvava ja ylhäältä rajoitettu, joten sillä on myös raja-arvo (joka on korkeintaan 1).

Lisäksi voidaan osoittaa, että tulojonon 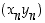, missä

raja-arvo on 1. Tästä seuraa, että

Siten on saatu, että