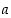 on
on 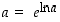 ,
voidaan tämän avulla yleinen eksponenttifunktio
,
voidaan tämän avulla yleinen eksponenttifunktio 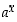 muuntaa tavalliseksi eksponenttifunktioksi seuraavasti:
muuntaa tavalliseksi eksponenttifunktioksi seuraavasti:
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
Koska jokaiselle positiiviselle luvulle 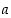 on
on 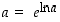 ,
voidaan tämän avulla yleinen eksponenttifunktio
,
voidaan tämän avulla yleinen eksponenttifunktio 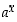 muuntaa tavalliseksi eksponenttifunktioksi seuraavasti:
muuntaa tavalliseksi eksponenttifunktioksi seuraavasti:
Tästä näkyy edelleen, että yleisen eksponenttifunktion derivaatta on
Sääntö 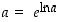 mahdollistaa myös yleisen potenssifunktion määrittelyn seuraavasti:
mahdollistaa myös yleisen potenssifunktion määrittelyn seuraavasti:
Näin ollen derivoimissääntö 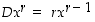 pätee kaikille reaalilukupotensseille, kun
pätee kaikille reaalilukupotensseille, kun 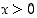 .
.
Yleinen logaritmifunktio 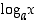 on yleisen eksponenttifunktion
on yleisen eksponenttifunktion 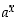 ,
,
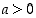 ,
käänteisfunktio. Koska
,
käänteisfunktio. Koska 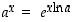 ,
saadaan sille lauseke
,
saadaan sille lauseke
Tästä saadaan edelleen sen derivaataksi
On huomattava, että yleiset eksponentti- ja logaritmifunktiot voidaan siten lausua tavallisten eksponentti- ja logaritmifunktioiden avulla.
Kantaluvulle 10 logaritmifunktion arvoa sanotaan myös Briggsin logaritmiksi ja siitä käytetään merkintää 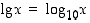 .
.
Tähän mennessä on käsitelty potenssilaskennan avulla muodostettuja funktioita, joissa joko kantaluku on muuttuva (potenssifunktiossa) tai potenssi on muuttuva (eksponenttifunktiossa). Mutta yleisemmin myös sellaiset potenssilausekkeet, joissa sekä kantaluku että potenssi ovat yhtaikaa muuttuvia, voidaan nyt määritellä eksponenttifunktion ja logaritmifunktion avulla seuraavasti.
Funktioille 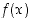 ja
ja 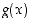 ,
missä
,
missä 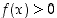 ,
asetetaan
,
asetetaan
Opiskelutehtävä 36. (Yleinen eksponenttifunktio)