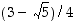 on luvun
on luvun 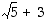 käänteisluku.
käänteisluku.
[Etusivu]
[Sisältö]
[Luku
I
II
III
IV
V
VI]
[Hakemisto]
[Ylempi pääsivu]
[Edellinen sivu]
[Seuraava sivu]
5. Osoita, että luku 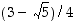 on luvun
on luvun 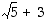 käänteisluku.
käänteisluku.
6. Osoita, että lausekkeiden 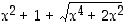 ja
ja 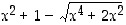 arvot ovat kaikilla reaaliluvuilla
arvot ovat kaikilla reaaliluvuilla 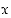 toistensa käänteislukuja.
toistensa käänteislukuja.
7. Millä muuttujan 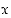 arvoilla luku
arvoilla luku 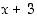 on luvun
on luvun 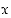 käänteisluku?
käänteisluku?
8. Osoita, että lukualue 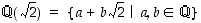 on suljettu yhteen-, vähennys-, kerto- ja jakolaskun suhteen ts. kahden tämän muotoisen luvun summa, erotus, tulo ja osamäärä (nollasta eroavalle jakajalle) ovat edelleen tämän muotoisia.
on suljettu yhteen-, vähennys-, kerto- ja jakolaskun suhteen ts. kahden tämän muotoisen luvun summa, erotus, tulo ja osamäärä (nollasta eroavalle jakajalle) ovat edelleen tämän muotoisia.
9. Osoita, että luku 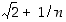 ei ole rationaaliluku, olipa
ei ole rationaaliluku, olipa 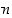 mikä tahansa nollasta eroava kokonaisluku.
mikä tahansa nollasta eroava kokonaisluku.
10. Määrää jokin kokonaislukukertoiminen polynomi, jolla on juurena luku 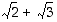 . (Apu: Määrää ensin luvun
. (Apu: Määrää ensin luvun 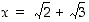 neliö. Yritä sitten päästä tulokseen jäävästä neliöjuuresta eroon sopivalla neliöön korottamisella. Tuloksena on neljännen asteen polynomi.)
neliö. Yritä sitten päästä tulokseen jäävästä neliöjuuresta eroon sopivalla neliöön korottamisella. Tuloksena on neljännen asteen polynomi.)
11. Osoita, että 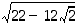 on muotoa
on muotoa 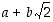 ,
missä
,
missä 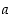 ja
ja 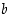 ovat rationaalilukuja.
ovat rationaalilukuja.
12. Voiko 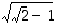 olla muotoa
olla muotoa 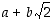 ,
missä
,
missä 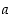 ja
ja 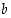 ovat rationaalilukuja?
ovat rationaalilukuja?
13. Osoita, että luku 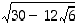 on muotoa
on muotoa 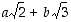 ,
missä
,
missä 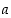 ja
ja 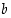 ovat rationaalilukuja.
ovat rationaalilukuja.
14. Lausu rationaaliluku 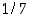 jaksollisena reaalilukuna. Tee sama luvuille
jaksollisena reaalilukuna. Tee sama luvuille 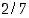 ja
ja 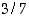 . Osoita jokin näistä esityksistä oikeaksi.
. Osoita jokin näistä esityksistä oikeaksi.
15. Muuta desimaaliluvut 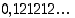 ja
ja 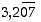 rationaaliluvuksi.
rationaaliluvuksi.
(a) Lausu desimaaliluku 1,2030303... murtolukuna.
(b) Konstruoi päättymätön jaksoton desimaaliluku.
17. Olkoon 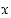 jaksollinen desimaaliluku, joka on muotoa
jaksollinen desimaaliluku, joka on muotoa 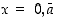 ,
missä toistuva jakso
,
missä toistuva jakso 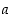 on yleisesti kokonaisluku, jolle
on yleisesti kokonaisluku, jolle 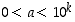 jollekin potenssille
jollekin potenssille 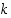 (joka osoittaa luvun
(joka osoittaa luvun 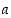 numeroiden määrän). Käyttäen geometrisen sarjan summakaavaa osoita, että luku
numeroiden määrän). Käyttäen geometrisen sarjan summakaavaa osoita, että luku 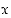 on rationaalinen.
on rationaalinen.
18. Olkoon reaaliluvulle 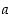 voimassa epäyhtälö
voimassa epäyhtälö 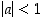 . Osoita, että
. Osoita, että 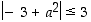 ja
ja 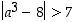 .
.
20. Muodostetaan reaaliluvulle 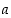 joukko
joukko 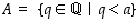 ja olkoon
ja olkoon 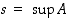 . Osoita, että
. Osoita, että 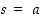 .
.
21. Selvitä, mikä on joukon 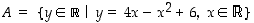 supremum. Onko sillä infimumia?
supremum. Onko sillä infimumia?
on infimum ja supremum? Määrää luvuista 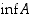 ,
,
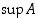 ,
,
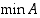 ja
ja 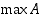 ne, jotka ovat olemassa.
ne, jotka ovat olemassa.
(a) Osoita, että joukko 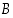 on rajoitettu.
on rajoitettu.
24. Osoita, että rationaaliluvun ja irrationaaliluvun summa ja (nollasta eroavien) tulo ovat irrationaalillukuja. (Vihje: Muodosta vastaväitteet.)
25. Osoita, että reaaliluvuille 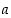 ja
ja 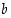 ,
joille
,
joille 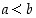 ,
on olemassa irrationaaliluku
,
on olemassa irrationaaliluku 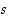 ,
jolle
,
jolle 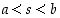 . (Apu: Katso lauseen 1.3.17 todistusta ja käytä nyt hyväksi sitä, että
. (Apu: Katso lauseen 1.3.17 todistusta ja käytä nyt hyväksi sitä, että 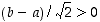 . Huomioi lisäksi edellinen harjoitustehtävä ja luvun
. Huomioi lisäksi edellinen harjoitustehtävä ja luvun 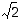 irrationaalisuus.)
irrationaalisuus.)