Irrationaaliluku
Sen lisäksi, että luku 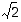 on erään polynomin juuri, sillä on eräs toinen ominaisuus, jota voidaan käyttää lukukäsitteen laajentamiseen. Se jakaa nimittäin rationaaliluvut kahtia sitä pienempiin lukuihin
on erään polynomin juuri, sillä on eräs toinen ominaisuus, jota voidaan käyttää lukukäsitteen laajentamiseen. Se jakaa nimittäin rationaaliluvut kahtia sitä pienempiin lukuihin 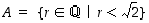 ja sitä isompiin lukuihin
ja sitä isompiin lukuihin 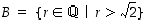 . On tietenkin olemassa paljon muitakin mahdollisuuksia jakaa rationaaliluvut sillä tavalla kahteen osajoukkoon
. On tietenkin olemassa paljon muitakin mahdollisuuksia jakaa rationaaliluvut sillä tavalla kahteen osajoukkoon 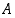 ja
ja 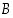 ,
että osajoukon
,
että osajoukon 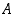 luvut ovat kaikkia osajoukon
luvut ovat kaikkia osajoukon 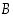 lukuja pienempiä, ts.
lukuja pienempiä, ts. 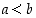 kaikilla
kaikilla 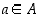 ja
ja 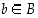 . Tällaisia rationaalilukujen jakoja sanotaan Dedekindin leikkauksiksi ja niiden avulla saadaankin muodostettua eräs malli reaaliluvuille. Esimerkiksi jako, jossa
. Tällaisia rationaalilukujen jakoja sanotaan Dedekindin leikkauksiksi ja niiden avulla saadaankin muodostettua eräs malli reaaliluvuille. Esimerkiksi jako, jossa
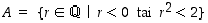 ja
ja 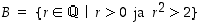 ,
,
vastaa lukua 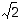 ,
sillä luku
,
sillä luku 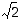 on joukkojen
on joukkojen 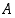 ja
ja 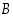 "välissä". Vaatii kuitenkin isohkon työn selvittää, miten näillä "leikkauksilla" tulee operoida, jotta ne toimisivat samoin laskuominaisuuksin kuin rationaaliluvut. Tämän asian käsittely sivuutetaan tässä.
"välissä". Vaatii kuitenkin isohkon työn selvittää, miten näillä "leikkauksilla" tulee operoida, jotta ne toimisivat samoin laskuominaisuuksin kuin rationaaliluvut. Tämän asian käsittely sivuutetaan tässä.
Jokainen rationaaliluku jakaa itse kaikkien rationaalilukujen joukon kahtia: ensimmäisen joukon muodostavat se ja sitä pienemmät luvut ja toisen sitä suuremmat luvut. Se määrää siten Dedekindin leikkauksen ja se voidaan siten käsittää erääksi reaaliluvuksi. Muita reaalilukuja kuin rationaalilukuja sanotaan irrationaaliluvuiksi. Esimerkin 1.3.1 mukaan luku 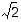 on irrationaalinen. Kaikista luvuista, kuten mm. luvuista
on irrationaalinen. Kaikista luvuista, kuten mm. luvuista 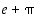 ja
ja 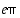 ,
ei tiedetä, ovatko ne rationaalisia vai irrationaalisia.
,
ei tiedetä, ovatko ne rationaalisia vai irrationaalisia.
Edeltä näkyy, että rationaalilukujen laajentaminen reaaliluvuiksi ei ole enää puhtaasti "algebrallinen" toimitus, vaan voi sanoa, että laajentaminen tapahtuu pikemminkin rationaalilukujen järjestysominaisuutta ja etäisyyskäsitettä hyödyntäen. Laajentamista voisi sanoa metriseksi täydentämiseksi (tai topologiseksi, kuten sitä yleisemmän teorian mukaan nimitetään).
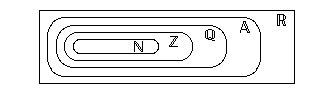
Yhteenvetona todetaan, että edellä käsitellyille reaalilukujen osajoukoille pätevät aidot sisältyvyydet 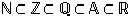 ,
missä
,
missä 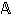 tarkoittaa algebrallisia lukuja (ks. kuva 2). Joukko
tarkoittaa algebrallisia lukuja (ks. kuva 2). Joukko 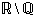 muodostuu kaikista irrationaalisista luvuista ja joukko
muodostuu kaikista irrationaalisista luvuista ja joukko 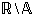 koostuu vastaavasti kaikista transkendenttisista luvuista.
koostuu vastaavasti kaikista transkendenttisista luvuista.
Kuva 2.
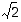 on erään polynomin juuri, sillä on eräs toinen ominaisuus, jota voidaan käyttää lukukäsitteen laajentamiseen. Se jakaa nimittäin rationaaliluvut kahtia sitä pienempiin lukuihin
on erään polynomin juuri, sillä on eräs toinen ominaisuus, jota voidaan käyttää lukukäsitteen laajentamiseen. Se jakaa nimittäin rationaaliluvut kahtia sitä pienempiin lukuihin 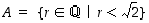 ja sitä isompiin lukuihin
ja sitä isompiin lukuihin 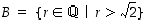 . On tietenkin olemassa paljon muitakin mahdollisuuksia jakaa rationaaliluvut sillä tavalla kahteen osajoukkoon
. On tietenkin olemassa paljon muitakin mahdollisuuksia jakaa rationaaliluvut sillä tavalla kahteen osajoukkoon 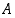 ja
ja 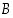 ,
että osajoukon
,
että osajoukon 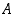 luvut ovat kaikkia osajoukon
luvut ovat kaikkia osajoukon 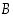 lukuja pienempiä, ts.
lukuja pienempiä, ts. 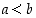 kaikilla
kaikilla 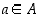 ja
ja 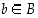 . Tällaisia rationaalilukujen jakoja sanotaan Dedekindin leikkauksiksi ja niiden avulla saadaankin muodostettua eräs malli reaaliluvuille. Esimerkiksi jako, jossa
. Tällaisia rationaalilukujen jakoja sanotaan Dedekindin leikkauksiksi ja niiden avulla saadaankin muodostettua eräs malli reaaliluvuille. Esimerkiksi jako, jossa 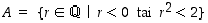 ja
ja 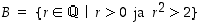 ,
,
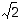 ,
sillä luku
,
sillä luku 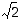 on joukkojen
on joukkojen 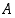 ja
ja 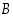 "välissä". Vaatii kuitenkin isohkon työn selvittää, miten näillä "leikkauksilla" tulee operoida, jotta ne toimisivat samoin laskuominaisuuksin kuin rationaaliluvut. Tämän asian käsittely sivuutetaan tässä.
"välissä". Vaatii kuitenkin isohkon työn selvittää, miten näillä "leikkauksilla" tulee operoida, jotta ne toimisivat samoin laskuominaisuuksin kuin rationaaliluvut. Tämän asian käsittely sivuutetaan tässä. 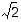 on irrationaalinen. Kaikista luvuista, kuten mm. luvuista
on irrationaalinen. Kaikista luvuista, kuten mm. luvuista 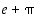 ja
ja 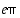 ,
ei tiedetä, ovatko ne rationaalisia vai irrationaalisia.
,
ei tiedetä, ovatko ne rationaalisia vai irrationaalisia. 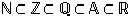 ,
missä
,
missä 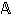 tarkoittaa algebrallisia lukuja (ks. kuva
tarkoittaa algebrallisia lukuja (ks. kuva 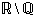 muodostuu kaikista irrationaalisista luvuista ja joukko
muodostuu kaikista irrationaalisista luvuista ja joukko 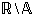 koostuu vastaavasti kaikista transkendenttisista luvuista.
koostuu vastaavasti kaikista transkendenttisista luvuista.