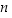 pätee:
pätee: 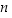 pätee:
pätee:
Koska yleisesti 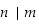 täsmälleen silloin, kun
täsmälleen silloin, kun 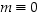 (mod
n
), voidaan väitteet esittää toisessa muodossa: a)
(mod
n
), voidaan väitteet esittää toisessa muodossa: a) 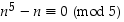 ,
b)
,
b) 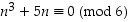 .
Tehdään todistukset modulolaskentaa käyttäen:
.
Tehdään todistukset modulolaskentaa käyttäen:
a) Koska alla olevassa taulukossa kaikille ekvivalenssiluokkien edustajille (vasen sarake) pätee, että lauseke 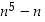 on kongruentti nollan kanssa (oikea sarake), niin väite pätee.
on kongruentti nollan kanssa (oikea sarake), niin väite pätee.
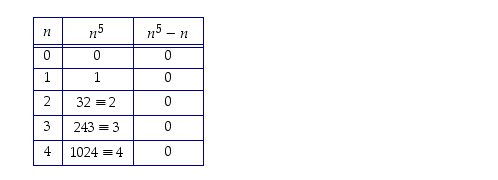
Väite pätee tämän mukaan itse asiassa kaikille kokonaisluvuille, ei vain luonnollisille luvuille.

Lisätietoja.
Vertaa tätä ratkaisua tehtävän 2.5 ratkaisuun. Siihen verraten tämä lähestymistapa toimii myös kaikkien kokonaislukujen joukossa 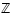 .
.